Question Number 123167 by Dwaipayan Shikari last updated on 23/Nov/20

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\sqrt{{n}}}{{n}^{\mathrm{2}} +{n}+\mathrm{1}} \\ $$
Commented by mathmax by abdo last updated on 23/Nov/20

$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\sqrt{\mathrm{n}}}{\mathrm{n}^{\mathrm{2}} \:+\mathrm{n}+\mathrm{1}}=\frac{\sqrt{\mathrm{1}}}{\mathrm{3}}\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}^{\mathrm{2}} \:+\mathrm{2}+\mathrm{1}}\:+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}^{\mathrm{2}} \:+\mathrm{3}+\mathrm{1}}+….. \\ $$
Answered by liberty last updated on 23/Nov/20
![Σ_(n=1) ^∞ ((√n)/((n+1+(√n))(n+1−(√n)))) Σ_(t=1) ^∞ (t/((t^2 +t+1)(t^2 −t+1))) (1/2)Σ_(t=1) ^∞ (((t^2 +t+1)−(t^2 −t+1))/((t^2 +t+1)(t^2 −t+1))) (1/2)[ Σ_(t=1) ^∞ (1/(t^2 −t+1))−(1/(t^2 +t+1)) ] (1/2) [ 1−(1/3)+(1/3)−(1/7)+(1/7)−(1/(13))+(1/(13))−(1/(21))+... +0−0 ] (1/2)×1=(1/2)](https://www.tinkutara.com/question/Q123170.png)
$$\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\sqrt{{n}}}{\left({n}+\mathrm{1}+\sqrt{{n}}\right)\left({n}+\mathrm{1}−\sqrt{{n}}\right)} \\ $$$$\:\underset{{t}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{t}}{\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{2}}\underset{{t}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)−\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)}{\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left[\:\underset{{t}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{t}^{\mathrm{2}} −{t}+\mathrm{1}}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}\:\right] \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:\left[\:\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{7}}+\frac{\mathrm{1}}{\mathrm{7}}−\frac{\mathrm{1}}{\mathrm{13}}+\frac{\mathrm{1}}{\mathrm{13}}−\frac{\mathrm{1}}{\mathrm{21}}+…\:+\mathrm{0}−\mathrm{0}\:\right] \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by Dwaipayan Shikari last updated on 23/Nov/20
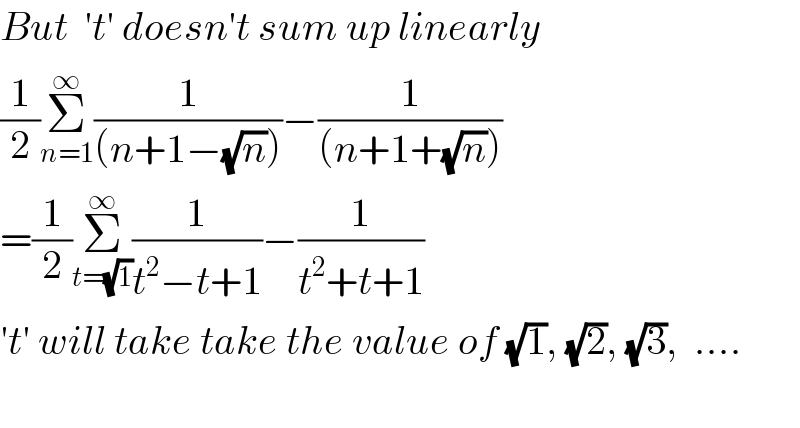
$${But}\:\:'{t}'\:{doesn}'{t}\:{sum}\:{up}\:{linearly}\:\: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}−\sqrt{{n}}\right)}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}+\sqrt{{n}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{t}=\sqrt{\mathrm{1}}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{t}^{\mathrm{2}} −{t}+\mathrm{1}}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}} \\ $$$$'{t}'\:{will}\:{take}\:{take}\:{the}\:{value}\:{of}\:\sqrt{\mathrm{1}},\:\sqrt{\mathrm{2}},\:\sqrt{\mathrm{3}},\:\:…. \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 23/Nov/20

$$\mathrm{answer}\:\mathrm{not}\:\mathrm{correct}\:\mathrm{you}\:\mathrm{can}\:\mathrm{not}\:\mathrm{use}\:\:\sqrt{\mathrm{n}}=\mathrm{t}\:\:\mathrm{in}\:\mathrm{sum}\:\mathrm{its}\:\mathrm{not}\:\mathrm{a}\:\mathrm{integral} \\ $$$$….! \\ $$
Commented by benjo_mathlover last updated on 23/Nov/20
![it should be Σ_(n=1) ^∞ ((√n)/((n+(√n)+1)(n−(√n)+1)))= Σ_(n=1) ^∞ (((n+(√n)+1)−(n−(√n)+1))/(2(n+(√n)+1)(n−(√n)+1)))= (1/2)Σ_(n=1) ^∞ (1/(n−(√n)+1)) − (1/(n+(√n)+1))= (1/2) [ 1−(1/3) + (1/(3−(√2)))−(1/(3+(√2)))+(1/(4−(√3)))−(1/(4+(√3)))+... ]](https://www.tinkutara.com/question/Q123196.png)
$${it}\:{should}\:{be}\: \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\sqrt{{n}}}{\left({n}+\sqrt{{n}}+\mathrm{1}\right)\left({n}−\sqrt{{n}}+\mathrm{1}\right)}= \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\left({n}+\sqrt{{n}}+\mathrm{1}\right)−\left({n}−\sqrt{{n}}+\mathrm{1}\right)}{\mathrm{2}\left({n}+\sqrt{{n}}+\mathrm{1}\right)\left({n}−\sqrt{{n}}+\mathrm{1}\right)}= \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{n}−\sqrt{{n}}+\mathrm{1}}\:−\:\frac{\mathrm{1}}{{n}+\sqrt{{n}}+\mathrm{1}}= \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:\left[\:\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\:+\:\frac{\mathrm{1}}{\mathrm{3}−\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{3}+\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\mathrm{4}−\sqrt{\mathrm{3}}}−\frac{\mathrm{1}}{\mathrm{4}+\sqrt{\mathrm{3}}}+…\:\right]\: \\ $$
