Question Number 122996 by Dwaipayan Shikari last updated on 21/Nov/20

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}}{{n}^{\mathrm{4}} +\mathrm{1}} \\ $$
Commented by Dwaipayan Shikari last updated on 21/Nov/20
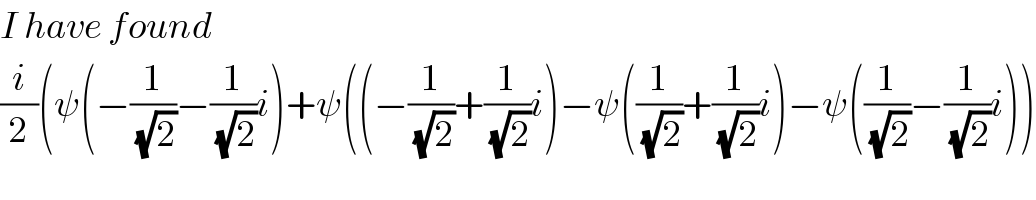
$${I}\:{have}\:{found} \\ $$$$\frac{{i}}{\mathrm{2}}\left(\psi\left(−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{i}\right)+\psi\left(\left(−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{i}\right)−\psi\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{i}\right)−\psi\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{i}\right)\right)\right. \\ $$
