Question Number 127793 by Dwaipayan Shikari last updated on 02/Jan/21
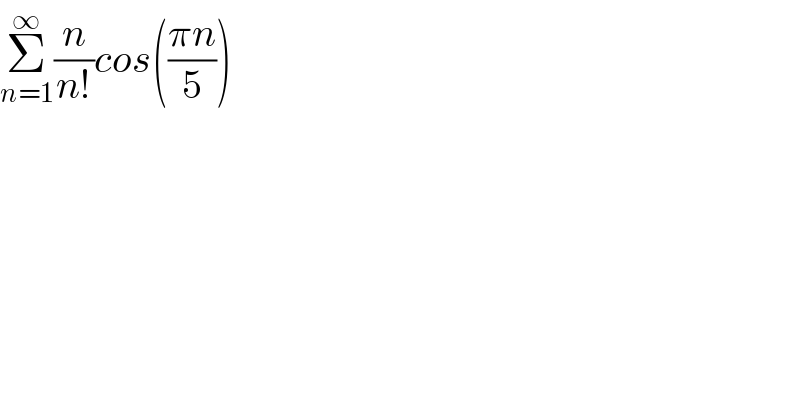
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}}{{n}!}{cos}\left(\frac{\pi{n}}{\mathrm{5}}\right) \\ $$
Commented by Dwaipayan Shikari last updated on 03/Jan/21
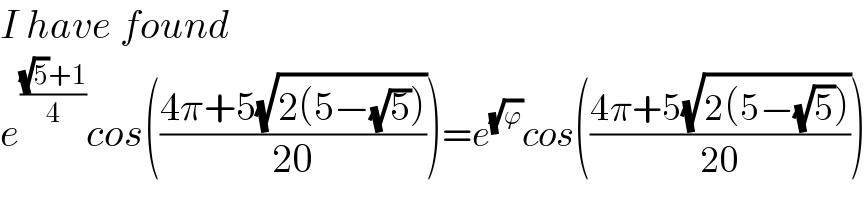
$${I}\:{have}\:{found} \\ $$$${e}^{\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}}} {cos}\left(\frac{\mathrm{4}\pi+\mathrm{5}\sqrt{\mathrm{2}\left(\mathrm{5}−\sqrt{\mathrm{5}}\right)}}{\mathrm{20}}\right)={e}^{\sqrt{\varphi}} {cos}\left(\frac{\mathrm{4}\pi+\mathrm{5}\sqrt{\mathrm{2}\left(\mathrm{5}−\sqrt{\mathrm{5}}\right)}}{\mathrm{20}}\right) \\ $$
Answered by mnjuly1970 last updated on 02/Jan/21
![Σ_(n=1) ^∞ (1/((n−1)!))cos(((nπ)/5)) =Re(Σ_(n=0) ^∞ (e^((i(n−1)π)/5) /(n!)))=Re(e^((−iπ)/5) Σ(e^((inπ)/5) /(n!))) =cos((π/5))Re[Σ_(n=0) ^∞ ((e^((inπ)/5) /(n!)) )] =cos((π/5))Re(e^(i(π/5)) )=cos^2 ((π/5)) =(((1+(√5) )/4))^2 =((6+2(√5) )/(16))=((3+(√5))/8)](https://www.tinkutara.com/question/Q127805.png)
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)!}{cos}\left(\frac{{n}\pi}{\mathrm{5}}\right) \\ $$$$={Re}\left(\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{e}^{\frac{{i}\left({n}−\mathrm{1}\right)\pi}{\mathrm{5}}} }{{n}!}\right)={Re}\left({e}^{\frac{−{i}\pi}{\mathrm{5}}} \Sigma\frac{{e}^{\frac{{in}\pi}{\mathrm{5}}} }{{n}!}\right) \\ $$$$={cos}\left(\frac{\pi}{\mathrm{5}}\right){Re}\left[\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{{e}^{\frac{{in}\pi}{\mathrm{5}}} }{{n}!}\:\right)\right] \\ $$$$={cos}\left(\frac{\pi}{\mathrm{5}}\right){Re}\left({e}^{{i}\frac{\pi}{\mathrm{5}}} \right)={cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{5}}\right) \\ $$$$=\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}\:}{\mathrm{4}}\right)^{\mathrm{2}} =\frac{\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}\:}{\mathrm{16}}=\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{8}} \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 02/Jan/21
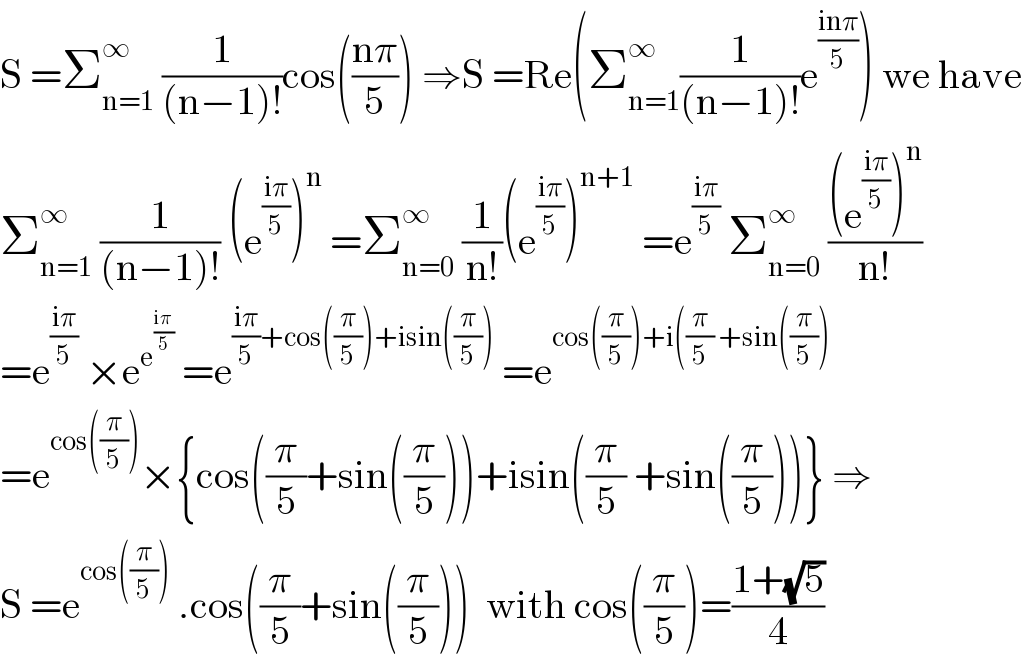
$$\mathrm{S}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{n}−\mathrm{1}\right)!}\mathrm{cos}\left(\frac{\mathrm{n}\pi}{\mathrm{5}}\right)\:\Rightarrow\mathrm{S}\:=\mathrm{Re}\left(\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{\left(\mathrm{n}−\mathrm{1}\right)!}\mathrm{e}^{\frac{\mathrm{in}\pi}{\mathrm{5}}} \right)\:\mathrm{we}\:\mathrm{have} \\ $$$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{n}−\mathrm{1}\right)!}\:\left(\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{5}}} \right)^{\mathrm{n}} \:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}!}\left(\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{5}}} \right)^{\mathrm{n}+\mathrm{1}} \:=\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{5}}} \:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{5}}} \right)^{\mathrm{n}} }{\mathrm{n}!} \\ $$$$=\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{5}}} \:×\mathrm{e}^{\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{5}}} } \:=\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{5}}+\mathrm{cos}\left(\frac{\pi}{\mathrm{5}}\right)+\mathrm{isin}\left(\frac{\pi}{\mathrm{5}}\right)} \:=\mathrm{e}^{\mathrm{cos}\left(\frac{\pi}{\mathrm{5}}\right)+\mathrm{i}\left(\frac{\pi}{\mathrm{5}}\:+\mathrm{sin}\left(\frac{\pi}{\mathrm{5}}\right)\right.} \\ $$$$=\mathrm{e}^{\mathrm{cos}\left(\frac{\pi}{\mathrm{5}}\right)} ×\left\{\mathrm{cos}\left(\frac{\pi}{\mathrm{5}}+\mathrm{sin}\left(\frac{\pi}{\mathrm{5}}\right)\right)+\mathrm{isin}\left(\frac{\pi}{\mathrm{5}}\:+\mathrm{sin}\left(\frac{\pi}{\mathrm{5}}\right)\right)\right\}\:\Rightarrow \\ $$$$\mathrm{S}\:=\mathrm{e}^{\mathrm{cos}\left(\frac{\pi}{\mathrm{5}}\right)} \:.\mathrm{cos}\left(\frac{\pi}{\mathrm{5}}+\mathrm{sin}\left(\frac{\pi}{\mathrm{5}}\right)\right)\:\:\mathrm{with}\:\mathrm{cos}\left(\frac{\pi}{\mathrm{5}}\right)=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$
