Question Number 167003 by cortano1 last updated on 04/Mar/22
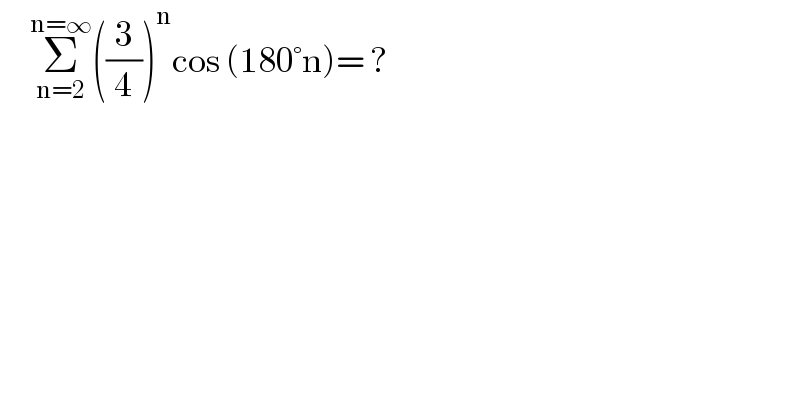
$$\:\:\:\:\:\underset{\mathrm{n}=\mathrm{2}} {\overset{\mathrm{n}=\infty} {\sum}}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{n}} \mathrm{cos}\:\left(\mathrm{180}°\mathrm{n}\right)=\:? \\ $$
Answered by greogoury55 last updated on 04/Mar/22
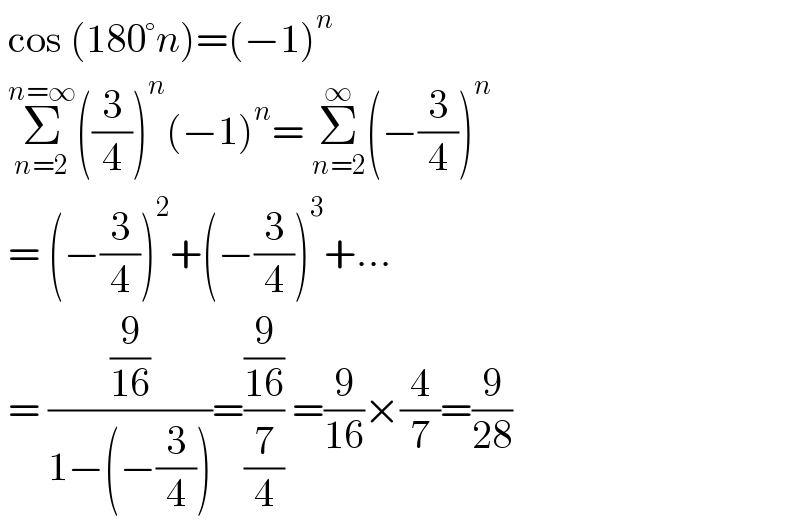
$$\:\mathrm{cos}\:\left(\mathrm{180}°{n}\right)=\left(−\mathrm{1}\right)^{{n}} \\ $$$$\:\underset{{n}=\mathrm{2}} {\overset{{n}=\infty} {\sum}}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{n}} \left(−\mathrm{1}\right)^{{n}} =\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\left(−\frac{\mathrm{3}}{\mathrm{4}}\right)^{{n}} \\ $$$$\:=\:\left(−\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} +\left(−\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{3}} +… \\ $$$$\:=\:\frac{\frac{\mathrm{9}}{\mathrm{16}}}{\mathrm{1}−\left(−\frac{\mathrm{3}}{\mathrm{4}}\right)}=\frac{\frac{\mathrm{9}}{\mathrm{16}}}{\frac{\mathrm{7}}{\mathrm{4}}}\:=\frac{\mathrm{9}}{\mathrm{16}}×\frac{\mathrm{4}}{\mathrm{7}}=\frac{\mathrm{9}}{\mathrm{28}}\: \\ $$
