Question Number 158522 by amin96 last updated on 05/Nov/21
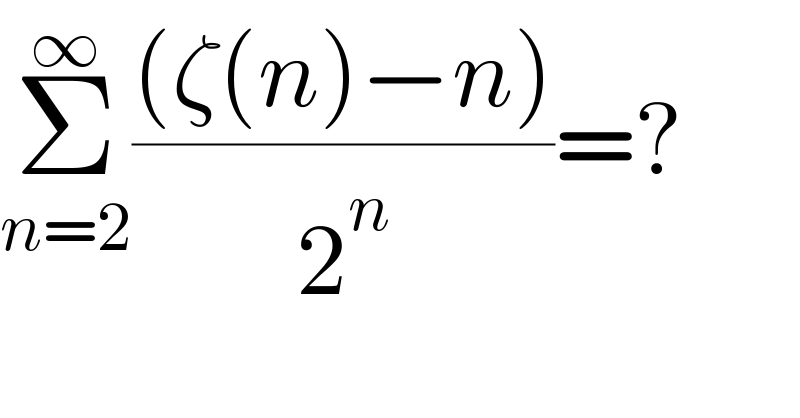
$$\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(\zeta\left({n}\right)−{n}\right)}{\mathrm{2}^{{n}} }=? \\ $$
Answered by qaz last updated on 06/Nov/21
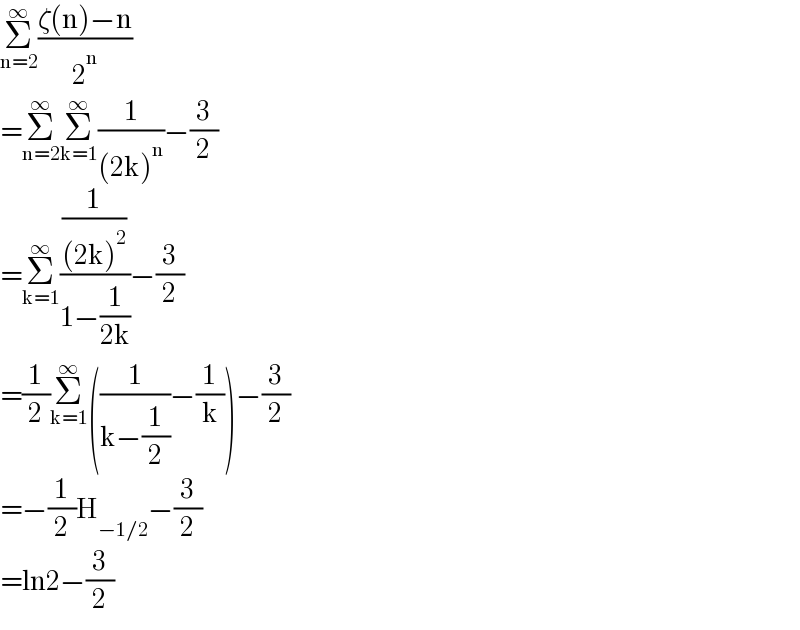
$$\underset{\mathrm{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\zeta\left(\mathrm{n}\right)−\mathrm{n}}{\mathrm{2}^{\mathrm{n}} } \\ $$$$=\underset{\mathrm{n}=\mathrm{2}} {\overset{\infty} {\sum}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2k}\right)^{\mathrm{n}} }−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$=\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\frac{\mathrm{1}}{\left(\mathrm{2k}\right)^{\mathrm{2}} }}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2k}}}−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{k}−\frac{\mathrm{1}}{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{k}}\right)−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{H}_{−\mathrm{1}/\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$=\mathrm{ln2}−\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by amin96 last updated on 06/Nov/21

$${thanks}\:{sir}.\:{very}\:{good}\:{solution} \\ $$
