n-is-an-integer-greater-than-1-Quantity-A-the-number-of-positive-divisor-of-2n-Quantity-B-twice-the-number-of-positive-divisors-of-n-

Question Number 178114 by aurpeyz last updated on 12/Oct/22

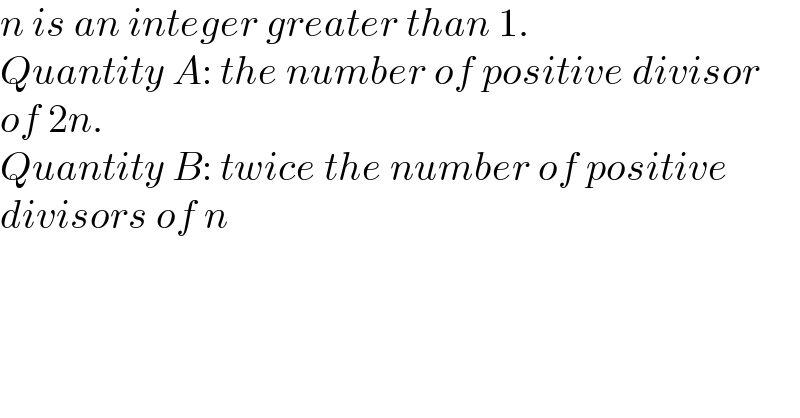
n i s a n i n t e g e r g r e a t e r t h a n 1 .

Q u a n t i t y A : t h e n u m b e r o f p o s i t i v e d i v i s o r

o f 2 n .

Q u a n t i t y B : t w i c e t h e n u m b e r o f p o s i t i v e

d i v i s o r s o f n

Commented by mr W last updated on 13/Oct/22

w h a t i s a s k e d ?

Answered by mr W last updated on 13/Oct/22

s a y n = p_{1}^{n_{1}} p_{2}^{n_{2}} \dots p_{k}^{n_{k}} w i t h p_{i} \in P

n u m b e r o f d i v i s o r s :

N (n) = (n_{1} + 1) (n_{2} + 1) \dots (n_{k} + 1)

2 n = 2^{1} p_{1}^{n_{1}} p_{2}^{n_{2}} \dots p_{k}^{n_{k}}

N (2 n) = (1 + 1) (n_{1} + 1) (n_{2} + 1) \dots (n_{k} + 1) i f p_{i} \neq 2

o r

N (2 n) = (n_{1} + 2) (n_{2} + 1) \dots (n_{k} + 1) i f p_{1} = 2

2 N (n) = 2 (n_{1} + 1) (n_{2} + 1) \dots (n_{k} + 1)

= N (2 n) i f p_{i} \neq 2

> N (2 n) i f p_{1} = 2

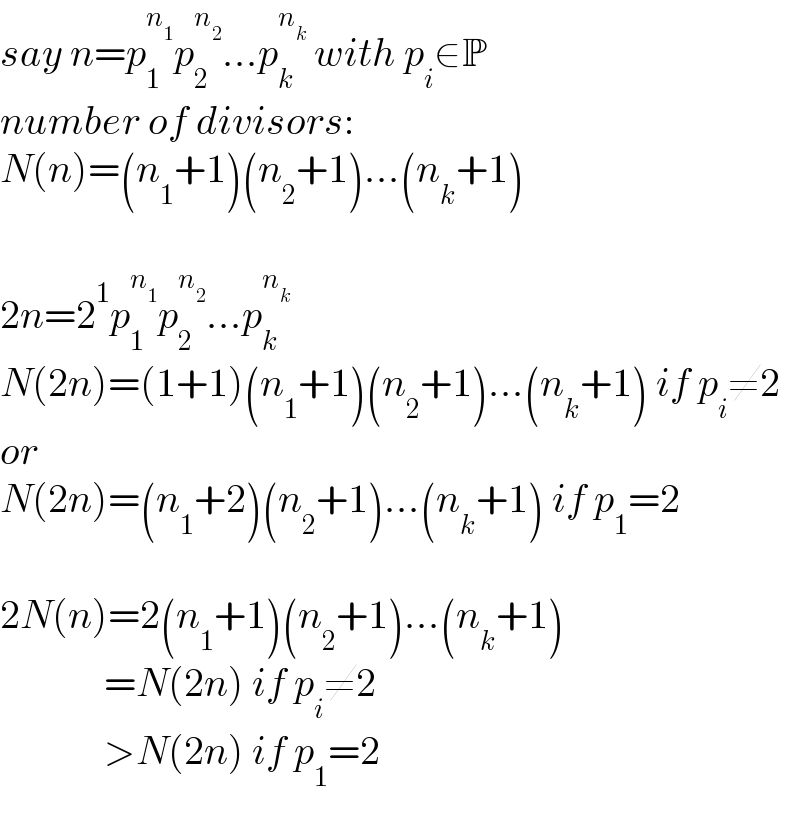
Commented by aurpeyz last updated on 13/Oct/22

a . Q u a n t i t y A i s g r e a t e r t h a n B

b . Q u a n t i t y B i s g r e a t e r t h a n A

c . t h e y a r e e q u a l

d . C a n n o t b e d e t e r m i n e d b y t h e g i v e n

i n f o r m a t i o n

Commented by mr W last updated on 13/Oct/22

a n s w e r d

Commented by mr W last updated on 13/Oct/22

e x a m p l e 1 : n = 15

n = 15 h a s 4 d i v i s o r s : 1, 3, 5, 15

2 n = 30 h a s 8 d i v i s o r s : 1, 2, 3, 4, 5, 6, 15, 30

Q n t . A = 8

Q n t . B = 2 \times 4 = 8

Q n t . A = Q n t . B

e x a m p l e 2 : n = 10

n = 10 h a s 4 d i v i s o r s : 1, 2, 5, 10

2 n = 20 h a s 6 d i v i s o r s : 1, 2, 4, 5, 10, 20

Q n t . A = 6

Q n t . B = 2 \times 4 = 8

Q n t . A < Q n t . B

Commented by Tawa11 last updated on 13/Oct/22

Great sir

Commented by aurpeyz last updated on 18/Oct/22

t h a n k s s i r

Facebook Tweet Pin