n-k-1-n-1-k-1-n-k-H-k-Find-the-value-of-n-1-1-n-1-n-2-

Question Number 156386 by mnjuly1970 last updated on 10/Oct/21

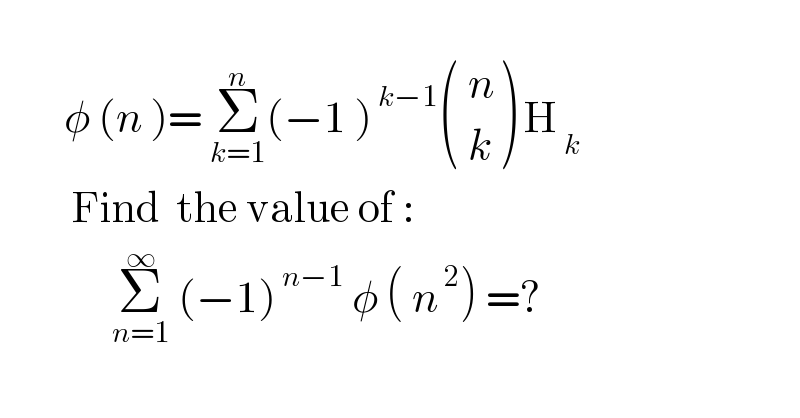
φ (n )= Σ_(k=1) ^n (−1 )^( k−1) ((( n)),(( k)) ) H_( k) Find the value of : Σ_(n=1) ^∞ (−1)^( n−1) φ ( n^( 2) ) =?

$$ \\ $$$$\:\:\:\:\:\:\:\:\phi\:\left({n}\:\right)=\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\:\right)^{\:{k}−\mathrm{1}} \begin{pmatrix}{\:{n}}\\{\:{k}}\end{pmatrix}\:\mathrm{H}_{\:{k}} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{Find}\:\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\left(−\mathrm{1}\right)^{\:{n}−\mathrm{1}} \:\phi\:\left(\:{n}^{\:\mathrm{2}} \right)\:=? \\ $$

Answered by mindispower last updated on 10/Oct/21

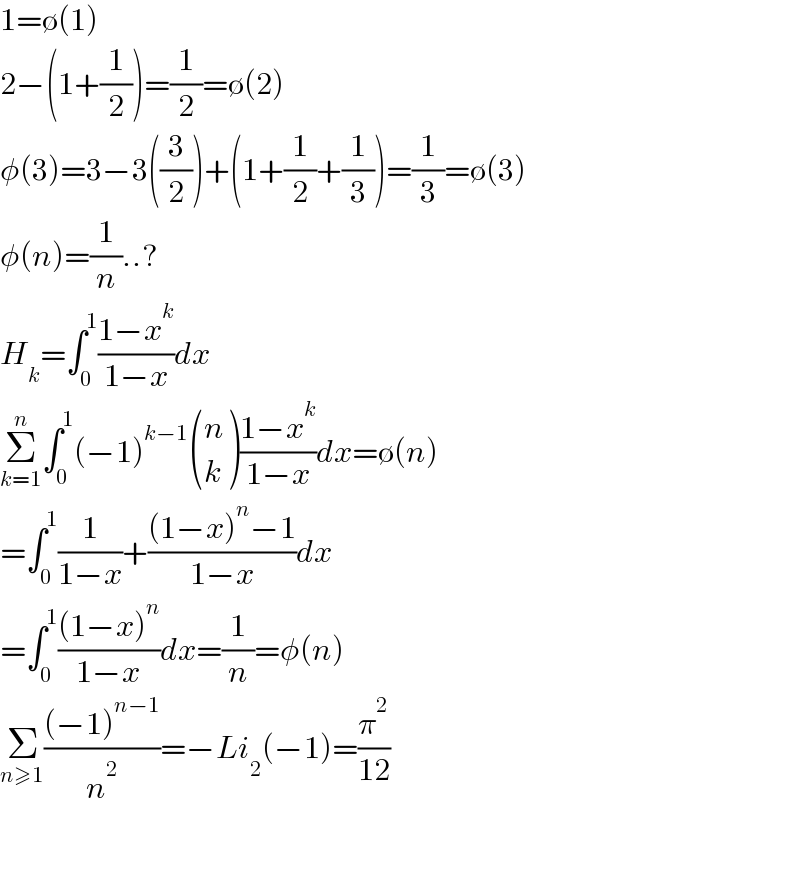
1=∅(1) 2−(1+(1/2))=(1/2)=∅(2) φ(3)=3−3((3/2))+(1+(1/2)+(1/3))=(1/3)=∅(3) φ(n)=(1/n)..? H_k =∫_0 ^1 ((1−x^k )/(1−x))dx Σ_(k=1) ^n ∫_0 ^1 (−1)^(k−1) ((n),(k) )((1−x^k )/(1−x))dx=∅(n) =∫_0 ^1 (1/(1−x))+(((1−x)^n −1)/(1−x))dx =∫_0 ^1 (((1−x)^n )/(1−x))dx=(1/n)=φ(n) Σ_(n≥1) (((−1)^(n−1) )/n^2 )=−Li_2 (−1)=(π^2 /(12))

$$\mathrm{1}=\emptyset\left(\mathrm{1}\right) \\ $$$$\mathrm{2}−\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{2}}=\emptyset\left(\mathrm{2}\right) \\ $$$$\phi\left(\mathrm{3}\right)=\mathrm{3}−\mathrm{3}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)+\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{1}}{\mathrm{3}}=\emptyset\left(\mathrm{3}\right) \\ $$$$\phi\left({n}\right)=\frac{\mathrm{1}}{{n}}..? \\ $$$${H}_{{k}} =\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}^{{k}} }{\mathrm{1}−{x}}{dx} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\frac{\mathrm{1}−{x}^{{k}} }{\mathrm{1}−{x}}{dx}=\emptyset\left({n}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}−{x}}+\frac{\left(\mathrm{1}−{x}\right)^{{n}} −\mathrm{1}}{\mathrm{1}−{x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−{x}\right)^{{n}} }{\mathrm{1}−{x}}{dx}=\frac{\mathrm{1}}{{n}}=\phi\left({n}\right) \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{2}} }=−{Li}_{\mathrm{2}} \left(−\mathrm{1}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$$ \\ $$$$ \\ $$

Commented by mnjuly1970 last updated on 10/Oct/21

$$\:\:{very}\:{nice}\:..{excellent}\:..{thank}\:{you} \\ $$$${so}\:{much}\:\:{sir}\:{power} \\ $$

Commented by mindispower last updated on 10/Oct/21

$${withe}\:{pleasur}\:{sir} \\ $$

Facebook Tweet Pin

n-k-1-n-1-k-1-n-k-H-k-Find-the-value-of-n-1-1-n-1-n-2-

Leave a Reply Cancel reply