n-N-prove-9-n-3-n-1-3-n-2-3-

Question Number 21067 by youssoufab last updated on 11/Sep/17

$$\forall{n}\in\mathbb{N},\:{prove}\:\mathrm{9}\mid\left[{n}^{\mathrm{3}} +\left({n}+\mathrm{1}\right)^{\mathrm{3}} +\left({n}+\mathrm{2}\right)^{\mathrm{3}} \right] \\ $$

Answered by dioph last updated on 12/Sep/17

n^3 +(n+1)^3 +(n+2)^3 = =n^3 +n^3 +3n^2 +3n+1+n^3 +6n^2 +12n+8= =3n^3 +9n^2 +15n+9 =3n(n^2 +5)+9(n^2 +1) = x Case 1: 3 ∣ n ⇒ n=3k ⇒ x=9k(9k^2 +5)+9(9k^2 +1) ⇒ 9 ∣ x Case 2: 3 ∤ n ⇒ n^2 +5 ≡ n^2 −1 ≡ (n+1)(n−1) ≡ 0 (mod 3) ⇒ n^2 +5 = 3h ⇒ x=9nh+9(n^2 +1) ⇒ 9 ∣ x ■

$${n}^{\mathrm{3}} +\left({n}+\mathrm{1}\right)^{\mathrm{3}} +\left({n}+\mathrm{2}\right)^{\mathrm{3}} = \\ $$$$={n}^{\mathrm{3}} +{n}^{\mathrm{3}} +\mathrm{3}{n}^{\mathrm{2}} +\mathrm{3}{n}+\mathrm{1}+{n}^{\mathrm{3}} +\mathrm{6}{n}^{\mathrm{2}} +\mathrm{12}{n}+\mathrm{8}= \\ $$$$=\mathrm{3}{n}^{\mathrm{3}} +\mathrm{9}{n}^{\mathrm{2}} +\mathrm{15}{n}+\mathrm{9} \\ $$$$=\mathrm{3}{n}\left({n}^{\mathrm{2}} +\mathrm{5}\right)+\mathrm{9}\left({n}^{\mathrm{2}} +\mathrm{1}\right)\:=\:{x} \\ $$$$\mathrm{Case}\:\mathrm{1}:\:\mathrm{3}\:\mid\:{n} \\ $$$$\Rightarrow\:{n}=\mathrm{3}{k} \\ $$$$\Rightarrow\:{x}=\mathrm{9}{k}\left(\mathrm{9}{k}^{\mathrm{2}} +\mathrm{5}\right)+\mathrm{9}\left(\mathrm{9}{k}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\Rightarrow\:\mathrm{9}\:\mid\:{x} \\ $$$$\mathrm{Case}\:\mathrm{2}:\:\mathrm{3}\:\nmid\:{n} \\ $$$$\Rightarrow\:{n}^{\mathrm{2}} +\mathrm{5}\:\equiv\:{n}^{\mathrm{2}} −\mathrm{1}\:\equiv\:\left({n}+\mathrm{1}\right)\left({n}−\mathrm{1}\right) \\ $$$$\equiv\:\mathrm{0}\:\left(\mathrm{mod}\:\mathrm{3}\right) \\ $$$$\Rightarrow\:{n}^{\mathrm{2}} +\mathrm{5}\:=\:\mathrm{3}{h} \\ $$$$\Rightarrow\:{x}=\mathrm{9}{nh}+\mathrm{9}\left({n}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\Rightarrow\:\mathrm{9}\:\mid\:{x} \\ $$$$\blacksquare \\ $$

Commented by youssoufab last updated on 14/Sep/17

$${thanks}\:{for}\:{help} \\ $$

Answered by mrW1 last updated on 12/Sep/17

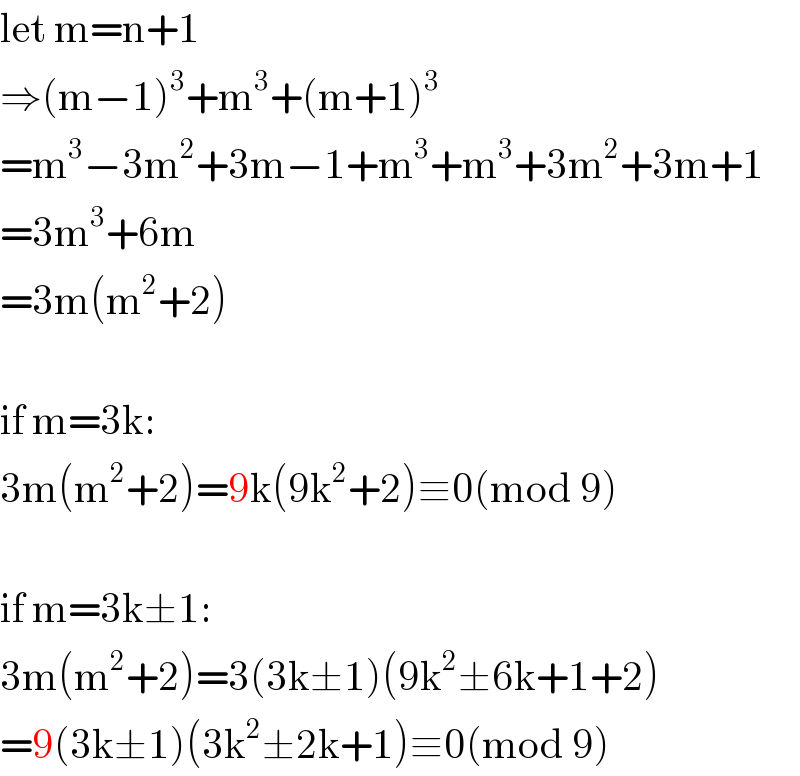
let m=n+1 ⇒(m−1)^3 +m^3 +(m+1)^3 =m^3 −3m^2 +3m−1+m^3 +m^3 +3m^2 +3m+1 =3m^3 +6m =3m(m^2 +2) if m=3k: 3m(m^2 +2)=9k(9k^2 +2)≡0(mod 9) if m=3k±1: 3m(m^2 +2)=3(3k±1)(9k^2 ±6k+1+2) =9(3k±1)(3k^2 ±2k+1)≡0(mod 9)

$$\mathrm{let}\:\mathrm{m}=\mathrm{n}+\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{m}−\mathrm{1}\right)^{\mathrm{3}} +\mathrm{m}^{\mathrm{3}} +\left(\mathrm{m}+\mathrm{1}\right)^{\mathrm{3}} \\ $$$$=\mathrm{m}^{\mathrm{3}} −\mathrm{3m}^{\mathrm{2}} +\mathrm{3m}−\mathrm{1}+\mathrm{m}^{\mathrm{3}} +\mathrm{m}^{\mathrm{3}} +\mathrm{3m}^{\mathrm{2}} +\mathrm{3m}+\mathrm{1} \\ $$$$=\mathrm{3m}^{\mathrm{3}} +\mathrm{6m} \\ $$$$=\mathrm{3m}\left(\mathrm{m}^{\mathrm{2}} +\mathrm{2}\right) \\ $$$$ \\ $$$$\mathrm{if}\:\mathrm{m}=\mathrm{3k}: \\ $$$$\mathrm{3m}\left(\mathrm{m}^{\mathrm{2}} +\mathrm{2}\right)=\mathrm{9k}\left(\mathrm{9k}^{\mathrm{2}} +\mathrm{2}\right)\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{9}\right) \\ $$$$ \\ $$$$\mathrm{if}\:\mathrm{m}=\mathrm{3k}\pm\mathrm{1}: \\ $$$$\mathrm{3m}\left(\mathrm{m}^{\mathrm{2}} +\mathrm{2}\right)=\mathrm{3}\left(\mathrm{3k}\pm\mathrm{1}\right)\left(\mathrm{9k}^{\mathrm{2}} \pm\mathrm{6k}+\mathrm{1}+\mathrm{2}\right) \\ $$$$=\mathrm{9}\left(\mathrm{3k}\pm\mathrm{1}\right)\left(\mathrm{3k}^{\mathrm{2}} \pm\mathrm{2k}+\mathrm{1}\right)\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{9}\right) \\ $$

Facebook Tweet Pin

n-N-prove-9-n-3-n-1-3-n-2-3-

Leave a Reply Cancel reply