Question Number 102480 by bemath last updated on 09/Jul/20
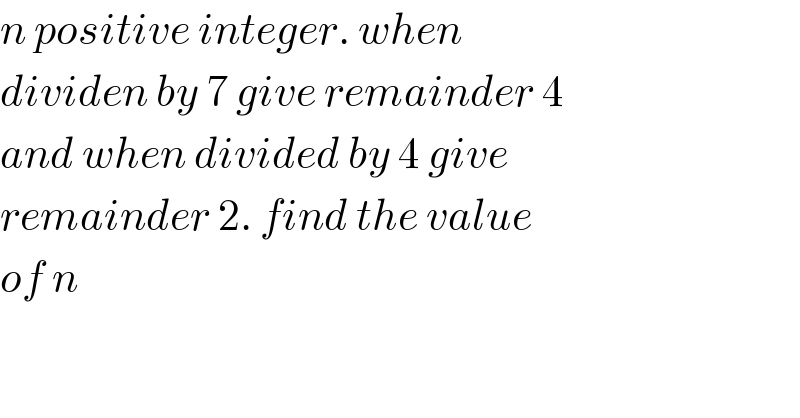
$${n}\:{positive}\:{integer}.\:{when} \\ $$$${dividen}\:{by}\:\mathrm{7}\:{give}\:{remainder}\:\mathrm{4} \\ $$$${and}\:{when}\:{divided}\:{by}\:\mathrm{4}\:{give} \\ $$$${remainder}\:\mathrm{2}.\:{find}\:{the}\:{value} \\ $$$${of}\:{n}\: \\ $$
Answered by nimnim last updated on 09/Jul/20
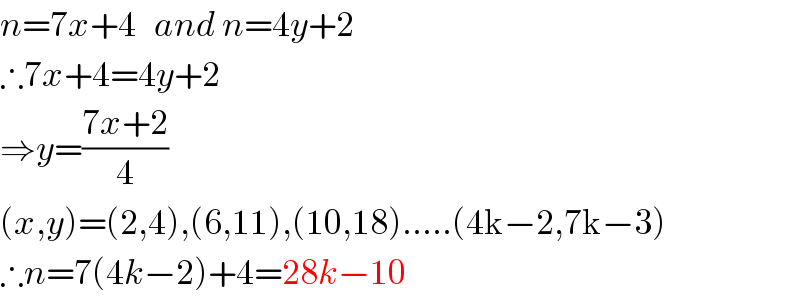
$${n}=\mathrm{7}{x}+\mathrm{4}\:\:\:{and}\:{n}=\mathrm{4}{y}+\mathrm{2} \\ $$$$\therefore\mathrm{7}{x}+\mathrm{4}=\mathrm{4}{y}+\mathrm{2} \\ $$$$\Rightarrow{y}=\frac{\mathrm{7}{x}+\mathrm{2}}{\mathrm{4}} \\ $$$$\left({x},{y}\right)=\left(\mathrm{2},\mathrm{4}\right),\left(\mathrm{6},\mathrm{11}\right),\left(\mathrm{10},\mathrm{18}\right)…..\left(\mathrm{4k}−\mathrm{2},\mathrm{7k}−\mathrm{3}\right) \\ $$$$\therefore{n}=\mathrm{7}\left(\mathrm{4}{k}−\mathrm{2}\right)+\mathrm{4}=\mathrm{28}{k}−\mathrm{10} \\ $$
Commented by bemath last updated on 09/Jul/20

$${okay}\:{sir} \\ $$
