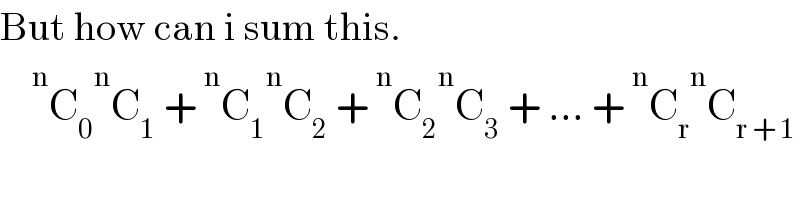Question Number 60406 by Tawa1 last updated on 20/May/19

Answered by mr W last updated on 20/May/19
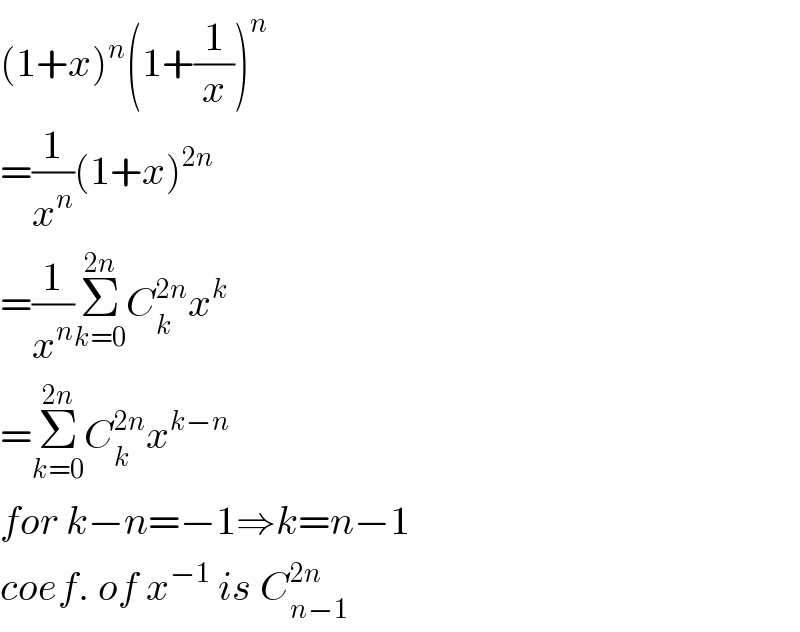
Commented by Tawa1 last updated on 20/May/19
Commented by Tawa1 last updated on 20/May/19
Commented by Tawa1 last updated on 20/May/19