Question Number 163463 by SANOGO last updated on 07/Jan/22
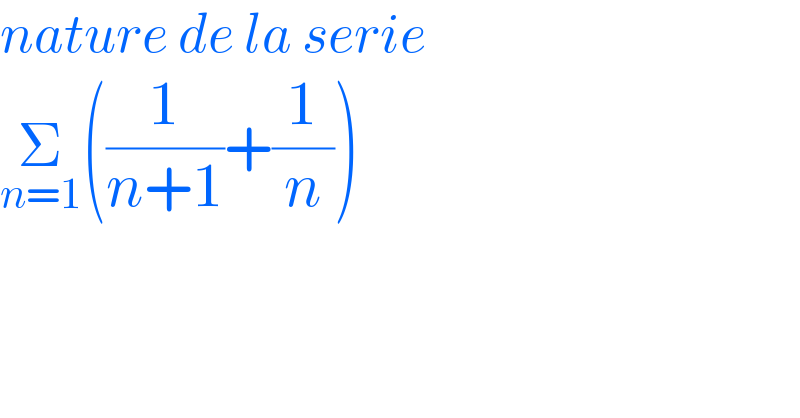
$${nature}\:{de}\:{la}\:{serie} \\ $$$$\underset{{n}=\mathrm{1}} {\sum}\left(\frac{\mathrm{1}}{{n}+\mathrm{1}}+\frac{\mathrm{1}}{{n}}\right) \\ $$
Answered by Ar Brandon last updated on 07/Jan/22
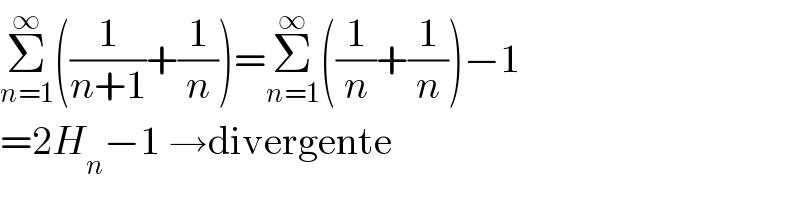
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}+\mathrm{1}}+\frac{\mathrm{1}}{{n}}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{{n}}\right)−\mathrm{1} \\ $$$$=\mathrm{2}{H}_{{n}} −\mathrm{1}\:\rightarrow\mathrm{divergente} \\ $$
Commented by SANOGO last updated on 07/Jan/22
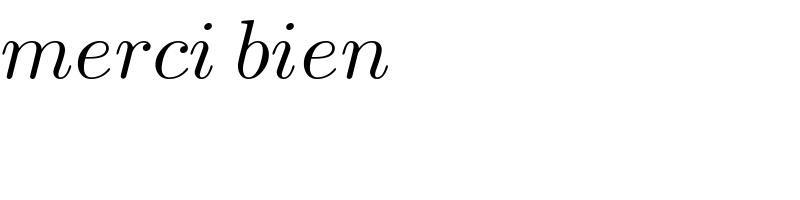
$${merci}\:{bien} \\ $$
