Question Number 162001 by SANOGO last updated on 25/Dec/21
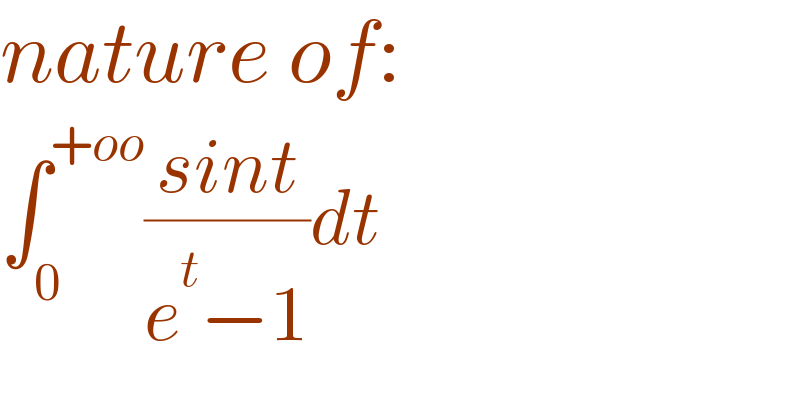
$${nature}\:{of}: \\ $$$$\int_{\mathrm{0}} ^{+{oo}} \frac{{sint}}{{e}^{{t}} −\mathrm{1}}{dt} \\ $$
Answered by mathmax by abdo last updated on 25/Dec/21
![Ψ=∫_0 ^∞ ((sint)/(e^t −1))dt ⇒Ψ=∫_0 ^∞ ((e^(−t) sint)/(1−e^(−t) ))dt =∫_0 ^∞ e^(−t) sint Σ_(n=0) ^∞ e^(−nt) dt =Σ_(n=0) ^∞ ∫_0 ^∞ e^(−(n+1)t) sint dt but ∫_0 ^∞ e^(−(n+1)t) sint dt =Im(∫_0 ^∞ e^(−(n+1)t+it) dt) and ∫_0 ^∞ e^((−(n+1)+i)t) dt =[(1/(−(n+1)+i))e^((−(n+1)+i)t) ]_0 ^∞ =−(1/(n+1−i))(−1) =(1/(n+1−i))=((n+1+i)/((n+1)^2 +1)) ⇒ Ψ=Σ_(n=0) ^∞ (1/((n+1)^2 +1))=Σ_(n=1) ^∞ (1/(n^2 +1)) et cette serie est convergente donc Ψ est cv.](https://www.tinkutara.com/question/Q162005.png)
$$\Psi=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{sint}}{\mathrm{e}^{\mathrm{t}} −\mathrm{1}}\mathrm{dt}\:\Rightarrow\Psi=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{t}} \mathrm{sint}}{\mathrm{1}−\mathrm{e}^{−\mathrm{t}} }\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}} \mathrm{sint}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{nt}} \mathrm{dt} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{t}} \mathrm{sint}\:\mathrm{dt} \\ $$$$\mathrm{but}\:\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{t}} \mathrm{sint}\:\mathrm{dt}\:=\mathrm{Im}\left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{t}+\mathrm{it}} \mathrm{dt}\right) \\ $$$$\mathrm{and}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\left(−\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{i}\right)\mathrm{t}} \mathrm{dt}\:=\left[\frac{\mathrm{1}}{−\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{i}}\mathrm{e}^{\left(−\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{i}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\infty} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}−\mathrm{i}}\left(−\mathrm{1}\right)\:=\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}−\mathrm{i}}=\frac{\mathrm{n}+\mathrm{1}+\mathrm{i}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}\:\Rightarrow \\ $$$$\Psi=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} +\mathrm{1}}\:\:\mathrm{et}\:\mathrm{cette}\:\mathrm{serie}\:\mathrm{est}\:\mathrm{convergente} \\ $$$$\mathrm{donc}\:\Psi\:\mathrm{est}\:\mathrm{cv}. \\ $$
Commented by Ar Brandon last updated on 25/Dec/21
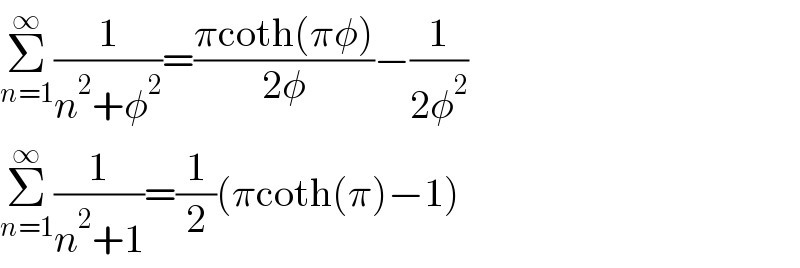
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\phi^{\mathrm{2}} }=\frac{\pi\mathrm{coth}\left(\pi\phi\right)}{\mathrm{2}\phi}−\frac{\mathrm{1}}{\mathrm{2}\phi^{\mathrm{2}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\pi\mathrm{coth}\left(\pi\right)−\mathrm{1}\right) \\ $$
Commented by SANOGO last updated on 25/Dec/21
$${merci}\:{bien} \\ $$
