Question Number 29500 by abdo imad last updated on 09/Feb/18
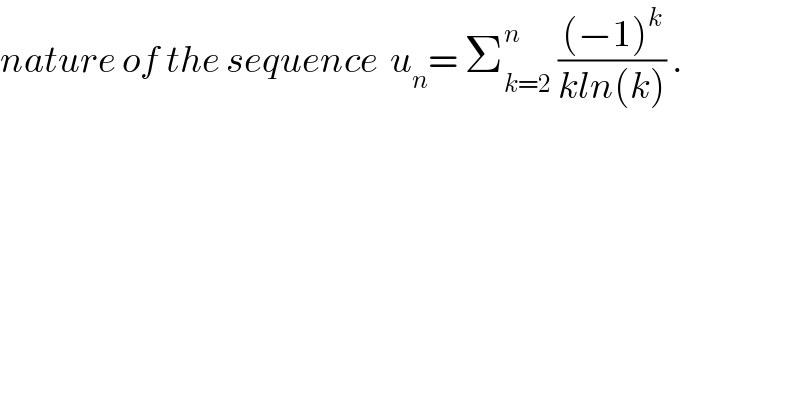
$${nature}\:{of}\:{the}\:{sequence}\:\:{u}_{{n}} =\:\sum_{{k}=\mathrm{2}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{kln}\left({k}\right)}\:. \\ $$
Commented by abdo imad last updated on 11/Feb/18
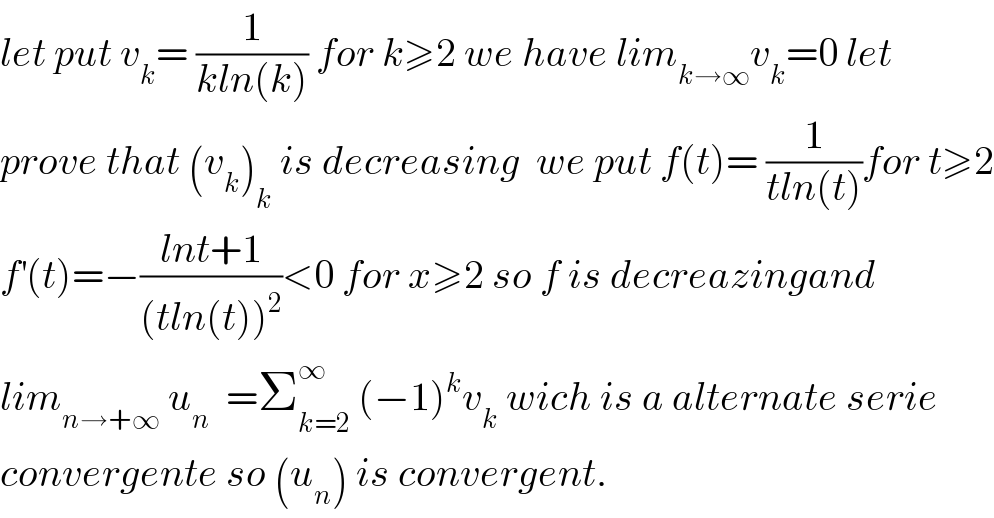
$${let}\:{put}\:{v}_{{k}} =\:\frac{\mathrm{1}}{{kln}\left({k}\right)}\:{for}\:{k}\geqslant\mathrm{2}\:{we}\:{have}\:{lim}_{{k}\rightarrow\infty} {v}_{{k}} =\mathrm{0}\:{let}\: \\ $$$${prove}\:{that}\:\left({v}_{{k}} \right)_{{k}} \:{is}\:{decreasing}\:\:{we}\:{put}\:{f}\left({t}\right)=\:\frac{\mathrm{1}}{{tln}\left({t}\right)}{for}\:{t}\geqslant\mathrm{2} \\ $$$${f}^{'} \left({t}\right)=−\frac{{lnt}+\mathrm{1}}{\left({tln}\left({t}\right)\right)^{\mathrm{2}} }<\mathrm{0}\:{for}\:{x}\geqslant\mathrm{2}\:{so}\:{f}\:{is}\:{decreazingand} \\ $$$${lim}_{{n}\rightarrow+\infty} \:{u}_{{n}} \:\:=\sum_{{k}=\mathrm{2}} ^{\infty} \:\left(−\mathrm{1}\right)^{{k}} {v}_{{k}} \:{wich}\:{is}\:{a}\:{alternate}\:{serie} \\ $$$${convergente}\:{so}\:\left({u}_{{n}} \right)\:{is}\:{convergent}. \\ $$
