Question Number 82452 by mathmax by abdo last updated on 21/Feb/20
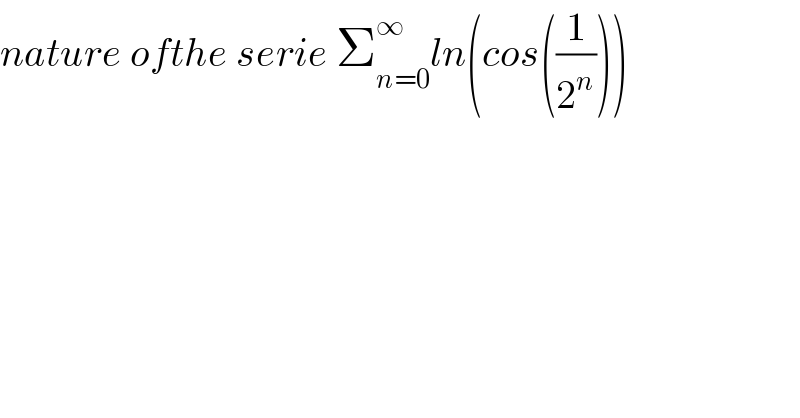
$${nature}\:{ofthe}\:{serie}\:\sum_{{n}=\mathrm{0}} ^{\infty} {ln}\left({cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right)\right) \\ $$
Commented by mathmax by abdo last updated on 23/Feb/20
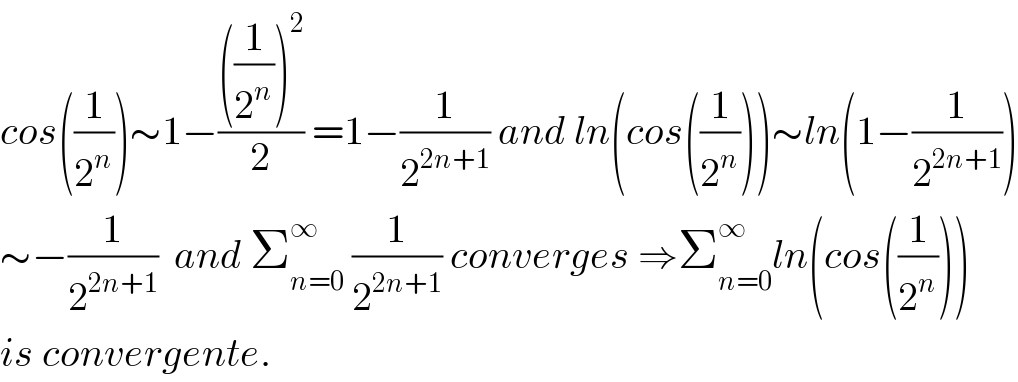
$${cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right)\sim\mathrm{1}−\frac{\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right)^{\mathrm{2}} }{\mathrm{2}}\:=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} }\:{and}\:{ln}\left({cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right)\right)\sim{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} }\right) \\ $$$$\sim−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} }\:\:{and}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} }\:{converges}\:\Rightarrow\sum_{{n}=\mathrm{0}} ^{\infty} {ln}\left({cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right)\right) \\ $$$${is}\:{convergente}. \\ $$
