Menu Close

new-attempt-to-solve-qu-37630-dx-x-x-1-x-2-t-x-1-dx-dt-dt-t-1-t-t-1-to-omit-the-roots-a-b-c-must-be-multiplied-with-a-

Tinku Tara 0 Comments
Pin




Question Number 38451 by MJS last updated on 25/Jun/18
new attempt to solve qu. 37630 ∫(dx/( (√x)+(√(x+1))+(√(x+2))))= [t=x+1 → dx=dt] =∫(dt/( (√(t−1))+(√t)+(√(t+1))))= [((to omit the roots)),(((√a)+(√b)+(√c) must be multiplied with)),(((−(√a)−(√b)+(√c))(−(√a)+(√b)−(√c))((√a)−(√b)−(√c)))),(((1/( (√a)+(√b)+(√c)))=((a^(3/2) +b^(3/2) +c^(3/2) +2(√(abc))−((a+b)(√c)+(a+c)(√b)+(b+c)(√a)))/(a^2 +b^2 +c^2 −2(ab+ac+bc))))) ] =∫((t(√(t−1))+t(√t)+t(√(t+1))+2(√(t−1))−2(√(t+1))−2(√((t−1)t(t+1))))/(3t^2 −4))dt= =∫((t(√(t−1)))/(3t^2 −4))dt+∫((t(√t))/(3t^2 −4))dt+∫((t(√(t+1)))/(3t^2 −4))dt+2∫((√(t−1))/(3t^2 −4))dt−2∫((√(t+1))/(3t^2 −4))−2∫((√((t−1)t(t+1)))/(3t^2 −4))dt I think I can solve them all except the last one so please somebody try ∫((√((t−1)t(t+1)))/(3t^2 −4))dt=? I will do the others tomorrow
$$\mathrm{new}\:\mathrm{attempt}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{qu}.\:\mathrm{37630} \\ $$$$ \\ $$$$\int\frac{{dx}}{\:\sqrt{{x}}+\sqrt{{x}+\mathrm{1}}+\sqrt{{x}+\mathrm{2}}}= \\ $$$$\:\:\:\:\:\left[{t}={x}+\mathrm{1}\:\rightarrow\:{dx}={dt}\right] \\ $$$$=\int\frac{{dt}}{\:\sqrt{{t}−\mathrm{1}}+\sqrt{{t}}+\sqrt{{t}+\mathrm{1}}}= \\ $$$$ \\ $$$$\:\:\:\:\:\begin{bmatrix}{\mathrm{to}\:\mathrm{omit}\:\mathrm{the}\:\mathrm{roots}}\\{\sqrt{{a}}+\sqrt{{b}}+\sqrt{{c}}\:\mathrm{must}\:\mathrm{be}\:\mathrm{multiplied}\:\mathrm{with}}\\{\left(−\sqrt{{a}}−\sqrt{{b}}+\sqrt{{c}}\right)\left(−\sqrt{{a}}+\sqrt{{b}}−\sqrt{{c}}\right)\left(\sqrt{{a}}−\sqrt{{b}}−\sqrt{{c}}\right)}\\{\frac{\mathrm{1}}{\:\sqrt{{a}}+\sqrt{{b}}+\sqrt{{c}}}=\frac{{a}^{\mathrm{3}/\mathrm{2}} +{b}^{\mathrm{3}/\mathrm{2}} +{c}^{\mathrm{3}/\mathrm{2}} +\mathrm{2}\sqrt{{abc}}−\left(\left({a}+{b}\right)\sqrt{{c}}+\left({a}+{c}\right)\sqrt{{b}}+\left({b}+{c}\right)\sqrt{{a}}\right)}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}\left({ab}+{ac}+{bc}\right)}}\end{bmatrix} \\ $$$$ \\ $$$$=\int\frac{{t}\sqrt{{t}−\mathrm{1}}+{t}\sqrt{{t}}+{t}\sqrt{{t}+\mathrm{1}}+\mathrm{2}\sqrt{{t}−\mathrm{1}}−\mathrm{2}\sqrt{{t}+\mathrm{1}}−\mathrm{2}\sqrt{\left({t}−\mathrm{1}\right){t}\left({t}+\mathrm{1}\right)}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}}{dt}= \\ $$$$=\int\frac{{t}\sqrt{{t}−\mathrm{1}}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}}{dt}+\int\frac{{t}\sqrt{{t}}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}}{dt}+\int\frac{{t}\sqrt{{t}+\mathrm{1}}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}}{dt}+\mathrm{2}\int\frac{\sqrt{{t}−\mathrm{1}}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}}{dt}−\mathrm{2}\int\frac{\sqrt{{t}+\mathrm{1}}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}}−\mathrm{2}\int\frac{\sqrt{\left({t}−\mathrm{1}\right){t}\left({t}+\mathrm{1}\right)}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}}{dt} \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{I}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{them}\:\mathrm{all}\:\mathrm{except}\:\mathrm{the}\:\mathrm{last}\:\mathrm{one} \\ $$$$\mathrm{so}\:\mathrm{please}\:\mathrm{somebody}\:\mathrm{try} \\ $$$$\int\frac{\sqrt{\left({t}−\mathrm{1}\right){t}\left({t}+\mathrm{1}\right)}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}}{dt}=? \\ $$$$\mathrm{I}\:\mathrm{will}\:\mathrm{do}\:\mathrm{the}\:\mathrm{others}\:\mathrm{tomorrow} \\ $$
Commented by math khazana by abdo last updated on 26/Jun/18
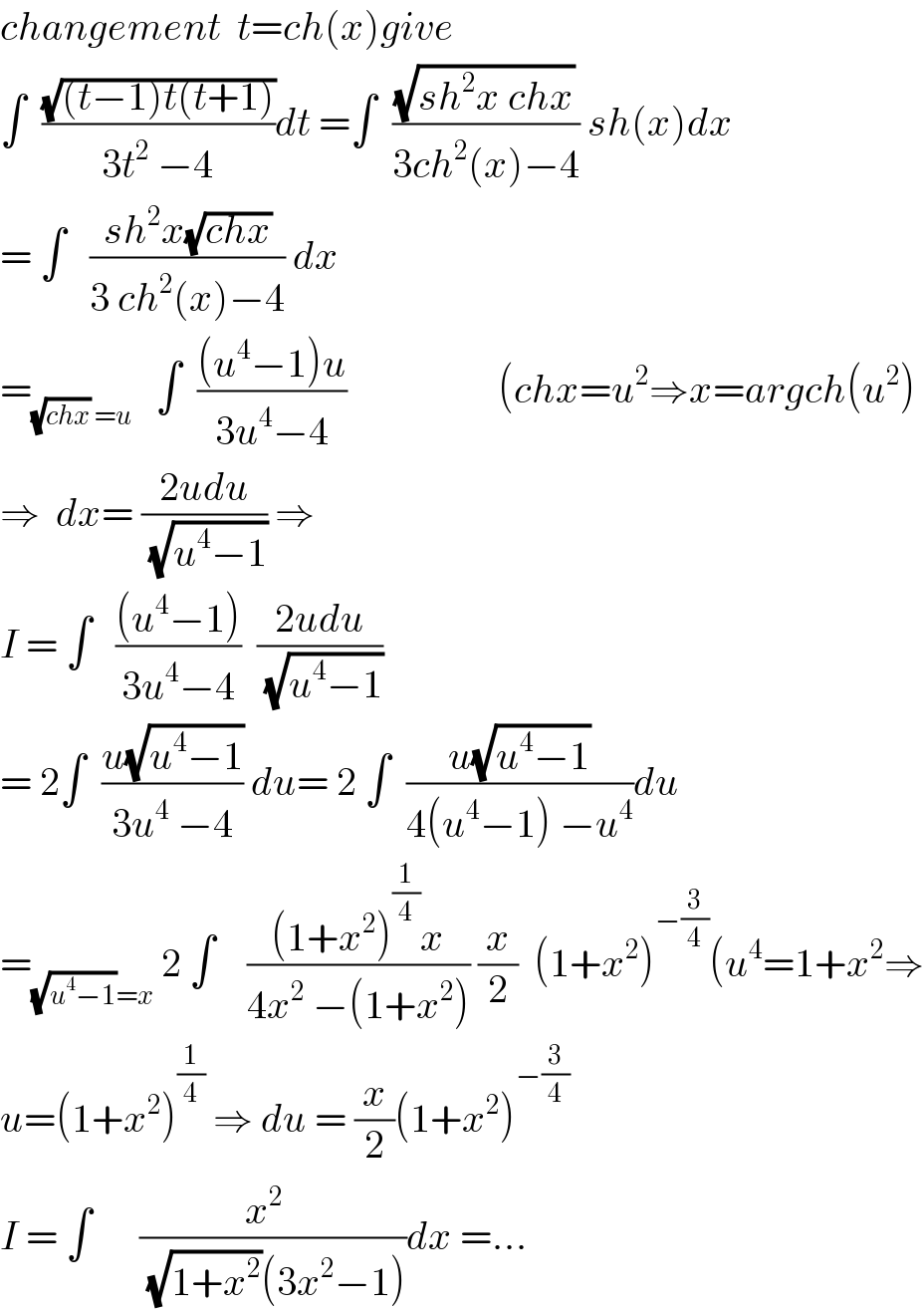
changement t=ch(x)give ∫ ((√((t−1)t(t+1)))/(3t^2 −4))dt =∫ ((√(sh^2 x chx))/(3ch^2 (x)−4)) sh(x)dx = ∫ ((sh^2 x(√(chx)))/(3 ch^2 (x)−4)) dx =_((√(chx)) =u) ∫ (((u^4 −1)u)/(3u^4 −4)) (chx=u^2 ⇒x=argch(u^2 ) ⇒ dx= ((2udu)/( (√(u^4 −1)))) ⇒ I = ∫ (((u^4 −1))/(3u^4 −4)) ((2udu)/( (√(u^4 −1)))) = 2∫ ((u(√(u^4 −1)))/(3u^4 −4)) du= 2 ∫ ((u(√(u^4 −1)))/(4(u^4 −1) −u^4 ))du =_((√(u^4 −1))=x) 2 ∫ (((1+x^2 )^(1/4) x)/(4x^2 −(1+x^2 ))) (x/2) (1+x^2 )^(−(3/4)) (u^4 =1+x^2 ⇒ u=(1+x^2 )^(1/4) ⇒ du = (x/2)(1+x^2 )^(−(3/4)) I = ∫ ((x^2 )/( (√(1+x^2 ))(3x^2 −1)))dx =...
$${changement}\:\:{t}={ch}\left({x}\right){give} \\ $$$$\int\:\:\frac{\sqrt{\left({t}−\mathrm{1}\right){t}\left({t}+\mathrm{1}\right)}}{\mathrm{3}{t}^{\mathrm{2}} \:−\mathrm{4}}{dt}\:=\int\:\:\frac{\sqrt{{sh}^{\mathrm{2}} {x}\:{chx}}}{\mathrm{3}{ch}^{\mathrm{2}} \left({x}\right)−\mathrm{4}}\:{sh}\left({x}\right){dx} \\ $$$$=\:\int\:\:\:\frac{{sh}^{\mathrm{2}} {x}\sqrt{{chx}}}{\mathrm{3}\:{ch}^{\mathrm{2}} \left({x}\right)−\mathrm{4}}\:{dx} \\ $$$$=_{\sqrt{{chx}}\:={u}} \:\:\:\int\:\:\frac{\left({u}^{\mathrm{4}} −\mathrm{1}\right){u}}{\mathrm{3}{u}^{\mathrm{4}} −\mathrm{4}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({chx}={u}^{\mathrm{2}} \Rightarrow{x}={argch}\left({u}^{\mathrm{2}} \right)\right. \\ $$$$\Rightarrow\:\:{dx}=\:\frac{\mathrm{2}{udu}}{\:\sqrt{{u}^{\mathrm{4}} −\mathrm{1}}}\:\Rightarrow \\ $$$${I}\:=\:\int\:\:\:\frac{\left({u}^{\mathrm{4}} −\mathrm{1}\right)}{\mathrm{3}{u}^{\mathrm{4}} −\mathrm{4}}\:\:\frac{\mathrm{2}{udu}}{\:\sqrt{{u}^{\mathrm{4}} −\mathrm{1}}} \\ $$$$=\:\mathrm{2}\int\:\:\frac{{u}\sqrt{{u}^{\mathrm{4}} −\mathrm{1}}}{\mathrm{3}{u}^{\mathrm{4}} \:−\mathrm{4}}\:{du}=\:\mathrm{2}\:\int\:\:\frac{{u}\sqrt{{u}^{\mathrm{4}} −\mathrm{1}}}{\mathrm{4}\left({u}^{\mathrm{4}} −\mathrm{1}\right)\:−{u}^{\mathrm{4}} }{du} \\ $$$$=_{\sqrt{{u}^{\mathrm{4}} −\mathrm{1}}={x}} \:\mathrm{2}\:\int\:\:\:\:\frac{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} {x}}{\mathrm{4}{x}^{\mathrm{2}} \:−\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:\frac{{x}}{\mathrm{2}}\:\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{3}}{\mathrm{4}}} \left({u}^{\mathrm{4}} =\mathrm{1}+{x}^{\mathrm{2}} \Rightarrow\right. \\ $$$${u}=\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} \:\Rightarrow\:{du}\:=\:\frac{{x}}{\mathrm{2}}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$${I}\:=\:\int\:\:\:\:\:\:\frac{{x}^{\mathrm{2}} \:\:}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}\right)}{dx}\:=… \\ $$
Answered by MJS last updated on 27/Jun/18
∫((t(√(t−1)))/(3t^2 −4))dt= [u=(√(t−1)) → dt=2(√(t−1))du] =2∫((u^4 +u^2 )/(3u^4 +6u^2 −1))du=(2/3)∫(1−((3u^2 −1)/(3u^4 +6u^2 −1)))du= =(2/3)∫du+(2/3)∫(du/(3u^4 +6u^2 −1))−2∫(u^2 /(3u^4 +6u^2 −1))du= (2/3)∫du=(2/3)u=(2/3)(√(t−1)) (2/3)∫(du/(3u^4 +6u^2 −1))=(2/9)∫(du/(u^4 +2u^2 −(1/3)))= =(2/9)∫(du/((u^2 +((3−2(√3))/3))(u^2 +((3+2(√3))/3))))= =(2/9)∫(A/(u^2 +((3−2(√3))/3)))du+(2/9)∫(B/(u^2 +((3+2(√3))/3)))du= =((√3)/(18))∫(du/(u^2 +((3−2(√3))/3)))−((√3)/(18))∫(du/(u^2 +((3+2(√3))/3)))= [∫(dv/(v^2 −p^2 ))=(1/(2p))ln ((v−p)/(v+p)); ∫(dv/(v^2 +q^2 ))=(1/q)arctan (v/q)] =((√3)/(36))(√(3+2(√3)))ln∣((u−((√3)/3)(√(−3+2(√3))))/(u+((√3)/3)(√(−3+2(√3)))))∣−((√3)/(18))(√(−3+2(√3)))arctan (√(−3+2(√3)))u= =((√3)/(36))((√(3+2(√3)))ln∣(((√(t−1))−((√3)/3)(√(−3+2(√3))))/( (√(t−1))+((√3)/3)(√(−3+2(√3)))))∣−2(√(−3+2(√3)))arctan (√((−3+2(√3))(t−1)))) −2∫(u^2 /(3u^4 +6u^2 −1))du=−(2/3)∫(u^2 /(u^4 +2u^2 −(1/3)))du= =−(2/3)∫(u^2 /((u^2 +((3−2(√3))/3))(u^2 +((3+2(√3))/3))))du= =−(2/3)∫(C/(u^2 +((3−2(√3))/3)))du−(2/3)∫(D/(u^2 +((3+2(√3))/3)))du= =−((2−(√3))/6)∫(du/(u^2 +((3−2(√3))/3)))−((2+(√3))/6)∫(du/(u^2 +((3+2(√3))/3)))= =−(1/(12))((√(−3+2(√3)))ln∣((u−((√3)/3)(√(−3+2(√3))))/(u+((√3)/3)(√(−3+2(√3)))))∣+2(√(3+2(√3)))arctan (√(−3+2(√3)))u)= =−(1/(12))((√(−3+2(√3)))ln∣(((√(t−1))−((√3)/3)(√(−3+2(√3))))/( (√(t−1))+((√3)/3)(√(−3+2(√3)))))∣+2(√(3+2(√3)))arctan (√((−3+2(√3))(t−1)))) =(2/3)(√(t−1))+((√3)/(18))(√(−3+2(√3)))ln∣(((√(t−1))−((√3)/3)(√(−3+2(√3))))/( (√(t−1))+((√3)/3)(√(−3+2(√3)))))∣+((√3)/9)(√(3+2(√3)))arctan (√((−3+2(√3))(t−1)))
$$\int\frac{{t}\sqrt{{t}−\mathrm{1}}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}}{dt}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{u}=\sqrt{{t}−\mathrm{1}}\:\rightarrow\:{dt}=\mathrm{2}\sqrt{{t}−\mathrm{1}}{du}\right] \\ $$$$=\mathrm{2}\int\frac{{u}^{\mathrm{4}} +{u}^{\mathrm{2}} }{\mathrm{3}{u}^{\mathrm{4}} +\mathrm{6}{u}^{\mathrm{2}} −\mathrm{1}}{du}=\frac{\mathrm{2}}{\mathrm{3}}\int\left(\mathrm{1}−\frac{\mathrm{3}{u}^{\mathrm{2}} −\mathrm{1}}{\mathrm{3}{u}^{\mathrm{4}} +\mathrm{6}{u}^{\mathrm{2}} −\mathrm{1}}\right){du}= \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\int{du}+\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{du}}{\mathrm{3}{u}^{\mathrm{4}} +\mathrm{6}{u}^{\mathrm{2}} −\mathrm{1}}−\mathrm{2}\int\frac{{u}^{\mathrm{2}} }{\mathrm{3}{u}^{\mathrm{4}} +\mathrm{6}{u}^{\mathrm{2}} −\mathrm{1}}{du}= \\ $$$$ \\ $$$$\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{3}}\int{du}=\frac{\mathrm{2}}{\mathrm{3}}{u}=\frac{\mathrm{2}}{\mathrm{3}}\sqrt{{t}−\mathrm{1}} \\ $$$$ \\ $$$$\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{du}}{\mathrm{3}{u}^{\mathrm{4}} +\mathrm{6}{u}^{\mathrm{2}} −\mathrm{1}}=\frac{\mathrm{2}}{\mathrm{9}}\int\frac{{du}}{{u}^{\mathrm{4}} +\mathrm{2}{u}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}}= \\ $$$$\:\:\:\:\:=\frac{\mathrm{2}}{\mathrm{9}}\int\frac{{du}}{\left({u}^{\mathrm{2}} +\frac{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\right)\left({u}^{\mathrm{2}} +\frac{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\right)}= \\ $$$$\:\:\:\:\:=\frac{\mathrm{2}}{\mathrm{9}}\int\frac{\mathcal{A}}{{u}^{\mathrm{2}} +\frac{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}}{du}+\frac{\mathrm{2}}{\mathrm{9}}\int\frac{\mathcal{B}}{{u}^{\mathrm{2}} +\frac{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}}{du}= \\ $$$$\:\:\:\:\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\int\frac{{du}}{{u}^{\mathrm{2}} +\frac{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\int\frac{{du}}{{u}^{\mathrm{2}} +\frac{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\int\frac{{dv}}{{v}^{\mathrm{2}} −{p}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}{p}}\mathrm{ln}\:\frac{{v}−{p}}{{v}+{p}};\:\int\frac{{dv}}{{v}^{\mathrm{2}} +{q}^{\mathrm{2}} }=\frac{\mathrm{1}}{{q}}\mathrm{arctan}\:\frac{{v}}{{q}}\right] \\ $$$$\:\:\:\:\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{36}}\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{ln}\mid\frac{{u}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}{{u}+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}\mid−\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{arctan}\:\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}{u}= \\ $$$$\:\:\:\:\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{36}}\left(\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{ln}\mid\frac{\sqrt{{t}−\mathrm{1}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}{\:\sqrt{{t}−\mathrm{1}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}\mid−\mathrm{2}\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{arctan}\:\sqrt{\left(−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}\right)\left({t}−\mathrm{1}\right)}\right) \\ $$$$ \\ $$$$\:\:\:\:\:−\mathrm{2}\int\frac{{u}^{\mathrm{2}} }{\mathrm{3}{u}^{\mathrm{4}} +\mathrm{6}{u}^{\mathrm{2}} −\mathrm{1}}{du}=−\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{u}^{\mathrm{2}} }{{u}^{\mathrm{4}} +\mathrm{2}{u}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}}{du}= \\ $$$$\:\:\:\:\:=−\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{u}^{\mathrm{2}} }{\left({u}^{\mathrm{2}} +\frac{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\right)\left({u}^{\mathrm{2}} +\frac{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\right)}{du}= \\ $$$$\:\:\:\:\:=−\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathcal{C}}{{u}^{\mathrm{2}} +\frac{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}}{du}−\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathcal{D}}{{u}^{\mathrm{2}} +\frac{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}}{du}= \\ $$$$\:\:\:\:\:=−\frac{\mathrm{2}−\sqrt{\mathrm{3}}}{\mathrm{6}}\int\frac{{du}}{{u}^{\mathrm{2}} +\frac{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}}−\frac{\mathrm{2}+\sqrt{\mathrm{3}}}{\mathrm{6}}\int\frac{{du}}{{u}^{\mathrm{2}} +\frac{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}}= \\ $$$$\:\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{12}}\left(\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{ln}\mid\frac{{u}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}{{u}+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}\mid+\mathrm{2}\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{arctan}\:\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}{u}\right)= \\ $$$$\:\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{12}}\left(\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{ln}\mid\frac{\sqrt{{t}−\mathrm{1}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}{\:\sqrt{{t}−\mathrm{1}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}\mid+\mathrm{2}\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{arctan}\:\sqrt{\left(−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}\right)\left({t}−\mathrm{1}\right)}\right) \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\sqrt{{t}−\mathrm{1}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{ln}\mid\frac{\sqrt{{t}−\mathrm{1}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}{\:\sqrt{{t}−\mathrm{1}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}\mid+\frac{\sqrt{\mathrm{3}}}{\mathrm{9}}\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{arctan}\:\sqrt{\left(−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}\right)\left({t}−\mathrm{1}\right)} \\ $$
Commented by MJS last updated on 27/Jun/18
∫((t(√(t+1)))/(3t^2 −4))dt= [same procedure as above] =(2/3)(√(t+1))+((√3)/(18))(√(3+2(√3)))ln∣(((√(t+1))−((√3)/3)(√(3+2(√3))))/( (√(t+1))+((√3)/3)(√(3+2(√3)))))∣−((√3)/9)(√(−3+2(√3)))arctan (√((3+2(√3))(t+1)))
$$\int\frac{{t}\sqrt{{t}+\mathrm{1}}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}}{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{same}\:\mathrm{procedure}\:\mathrm{as}\:\mathrm{above}\right] \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\sqrt{{t}+\mathrm{1}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{ln}\mid\frac{\sqrt{{t}+\mathrm{1}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}{\:\sqrt{{t}+\mathrm{1}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}\mid−\frac{\sqrt{\mathrm{3}}}{\mathrm{9}}\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{arctan}\:\sqrt{\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}\right)\left({t}+\mathrm{1}\right)} \\ $$
Commented by MJS last updated on 27/Jun/18
∫((t(√t))/(3t^2 −4))dt= [ditto] =(2/3)(√t)+((√(6(√3)))/(18))ln∣(((√t)−((√(6(√3)))/3))/( (√t)+((√(6(√3)))/3)))∣−((√(6(√3)))/9)arctan ((√(2(√3)t))/2)
$$\int\frac{{t}\sqrt{{t}}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}}{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{ditto}\right] \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\sqrt{{t}}+\frac{\sqrt{\mathrm{6}\sqrt{\mathrm{3}}}}{\mathrm{18}}\mathrm{ln}\mid\frac{\sqrt{{t}}−\frac{\sqrt{\mathrm{6}\sqrt{\mathrm{3}}}}{\mathrm{3}}}{\:\sqrt{{t}}+\frac{\sqrt{\mathrm{6}\sqrt{\mathrm{3}}}}{\mathrm{3}}}\mid−\frac{\sqrt{\mathrm{6}\sqrt{\mathrm{3}}}}{\mathrm{9}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{2}\sqrt{\mathrm{3}}{t}}}{\mathrm{2}} \\ $$
Commented by MJS last updated on 27/Jun/18
2∫((√(t−1))/(3t^2 −4))dt= =(1/6)(√(−3+2(√3)))ln∣(((√(t−1))−((√3)/3)(√(−3+2(√3))))/( (√(t−1))+((√3)/3)(√(−3+2(√3)))))∣−(1/3)(√(3+2(√3)))arctan (√((−3+2(√3))(t−1))) −2∫((√(t+1))/(3t^2 −4))dt= =−(1/6)(√(3+2(√3)))ln∣(((√(t+1))−((√3)/3)(√(3+2(√3))))/( (√(t+1))+((√3)/3)(√(3+2(√3)))))∣−(1/3)(√(−3+2(√3)))arctan (√((3+2(√3))(t+1)))
$$\mathrm{2}\int\frac{\sqrt{{t}−\mathrm{1}}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}}{dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{ln}\mid\frac{\sqrt{{t}−\mathrm{1}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}{\:\sqrt{{t}−\mathrm{1}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}\mid−\frac{\mathrm{1}}{\mathrm{3}}\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{arctan}\:\sqrt{\left(−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}\right)\left({t}−\mathrm{1}\right)} \\ $$$$−\mathrm{2}\int\frac{\sqrt{{t}+\mathrm{1}}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}}{dt}= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{6}}\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{ln}\mid\frac{\sqrt{{t}+\mathrm{1}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}{\:\sqrt{{t}+\mathrm{1}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}\mid−\frac{\mathrm{1}}{\mathrm{3}}\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{arctan}\:\sqrt{\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}\right)\left({t}+\mathrm{1}\right)} \\ $$
Commented by MJS last updated on 27/Jun/18
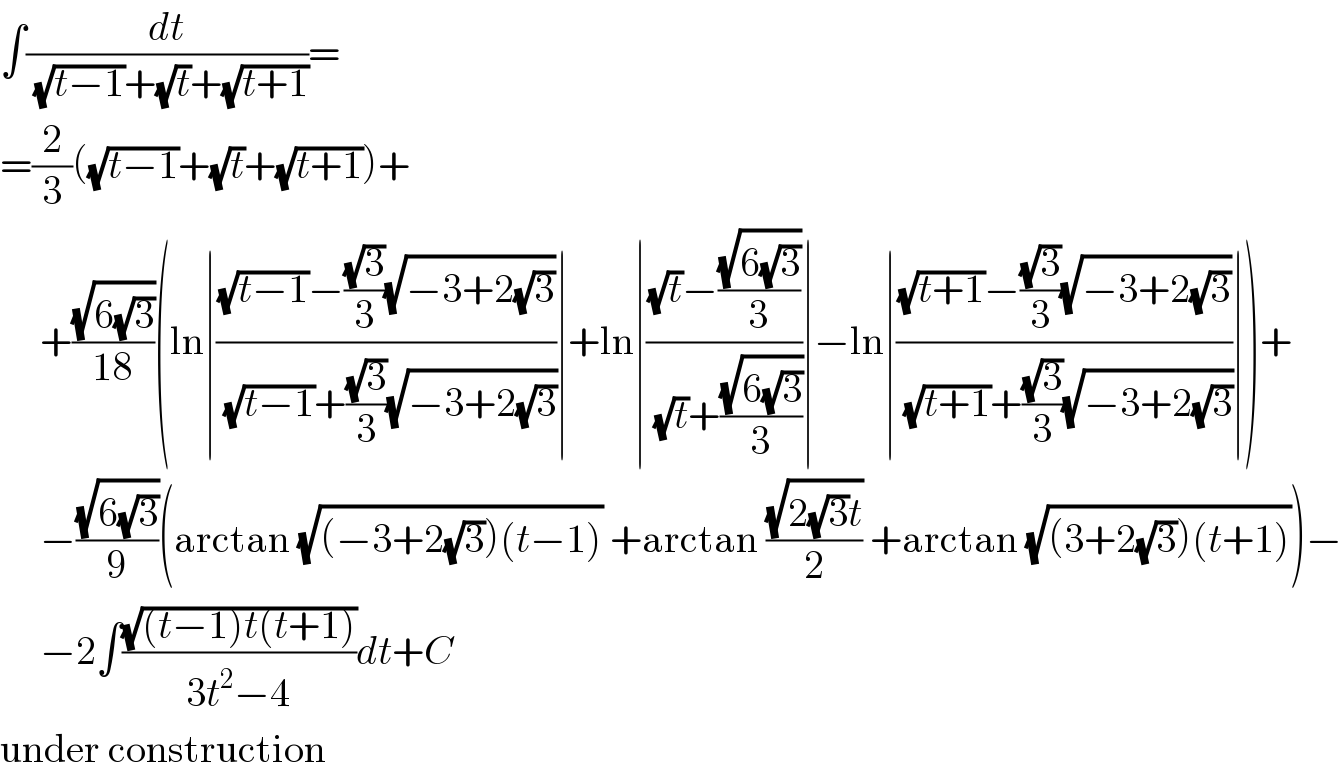
∫(dt/( (√(t−1))+(√t)+(√(t+1))))= =(2/3)((√(t−1))+(√t)+(√(t+1)))+ +((√(6(√3)))/(18))(ln∣(((√(t−1))−((√3)/3)(√(−3+2(√3))))/( (√(t−1))+((√3)/3)(√(−3+2(√3)))))∣+ln∣(((√t)−((√(6(√3)))/3))/( (√t)+((√(6(√3)))/3)))∣−ln∣(((√(t+1))−((√3)/3)(√(−3+2(√3))))/( (√(t+1))+((√3)/3)(√(−3+2(√3)))))∣)+ −((√(6(√3)))/9)(arctan (√((−3+2(√3))(t−1))) +arctan ((√(2(√3)t))/2) +arctan (√((3+2(√3))(t+1))))− −2∫((√((t−1)t(t+1)))/(3t^2 −4))dt+C under construction
$$\int\frac{{dt}}{\:\sqrt{{t}−\mathrm{1}}+\sqrt{{t}}+\sqrt{{t}+\mathrm{1}}}= \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\left(\sqrt{{t}−\mathrm{1}}+\sqrt{{t}}+\sqrt{{t}+\mathrm{1}}\right)+ \\ $$$$\:\:\:\:\:+\frac{\sqrt{\mathrm{6}\sqrt{\mathrm{3}}}}{\mathrm{18}}\left(\mathrm{ln}\mid\frac{\sqrt{{t}−\mathrm{1}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}{\:\sqrt{{t}−\mathrm{1}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}\mid+\mathrm{ln}\mid\frac{\sqrt{{t}}−\frac{\sqrt{\mathrm{6}\sqrt{\mathrm{3}}}}{\mathrm{3}}}{\:\sqrt{{t}}+\frac{\sqrt{\mathrm{6}\sqrt{\mathrm{3}}}}{\mathrm{3}}}\mid−\mathrm{ln}\mid\frac{\sqrt{{t}+\mathrm{1}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}{\:\sqrt{{t}+\mathrm{1}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}\mid\right)+ \\ $$$$\:\:\:\:\:−\frac{\sqrt{\mathrm{6}\sqrt{\mathrm{3}}}}{\mathrm{9}}\left(\mathrm{arctan}\:\sqrt{\left(−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}\right)\left({t}−\mathrm{1}\right)}\:+\mathrm{arctan}\:\frac{\sqrt{\mathrm{2}\sqrt{\mathrm{3}}{t}}}{\mathrm{2}}\:+\mathrm{arctan}\:\sqrt{\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}\right)\left({t}+\mathrm{1}\right)}\right)− \\ $$$$\:\:\:\:\:−\mathrm{2}\int\frac{\sqrt{\left({t}−\mathrm{1}\right){t}\left({t}+\mathrm{1}\right)}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}}{dt}+{C} \\ $$$$\mathrm{under}\:\mathrm{construction} \\ $$
Commented by math khazana by abdo last updated on 27/Jun/18
sir Mjs you are really tired with this itegral thank youfor thishard work you are really patient...
$${sir}\:{Mjs}\:{you}\:{are}\:{really}\:{tired}\:{with}\:{this}\:{itegral} \\ $$$${thank}\:{youfor}\:{thishard}\:{work}\:\:{you}\:{are}\:{really} \\ $$$${patient}… \\ $$
Commented by MJS last updated on 27/Jun/18
this integral is my personal nemesis LOL
$$\mathrm{this}\:\mathrm{integral}\:\mathrm{is}\:\mathrm{my}\:\mathrm{personal}\:\mathrm{nemesis}\:\mathrm{LOL} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *