Menu Close

Nice-1-ln-2-x-x-ln-x-dx-x-1-x-3-dx-4-x-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 127237 by bramlexs22 last updated on 28/Dec/20
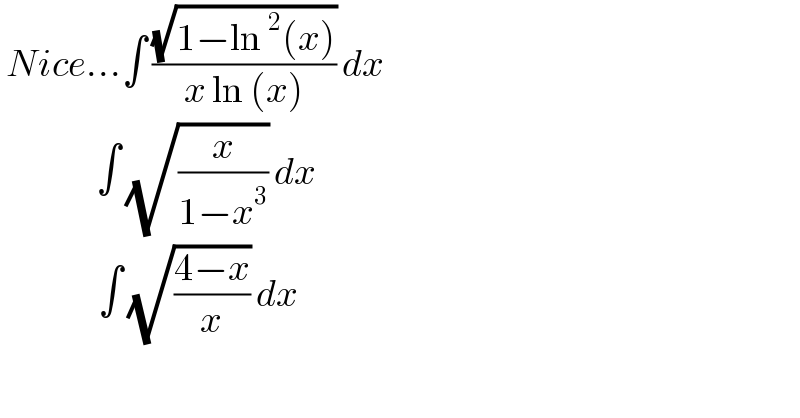
Nice...∫ ((√(1−ln^2 (x)))/(x ln (x))) dx ∫ (√(x/(1−x^3 ))) dx ∫ (√((4−x)/x)) dx
$$\:{Nice}…\int\:\frac{\sqrt{\mathrm{1}−\mathrm{ln}\:^{\mathrm{2}} \left({x}\right)}}{{x}\:\mathrm{ln}\:\left({x}\right)}\:{dx}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int\:\sqrt{\frac{{x}}{\mathrm{1}−{x}^{\mathrm{3}} }}\:{dx}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\int\:\sqrt{\frac{\mathrm{4}−{x}}{{x}}}\:{dx}\: \\ $$
Commented by bramlexs22 last updated on 28/Dec/20
Answered by liberty last updated on 28/Dec/20
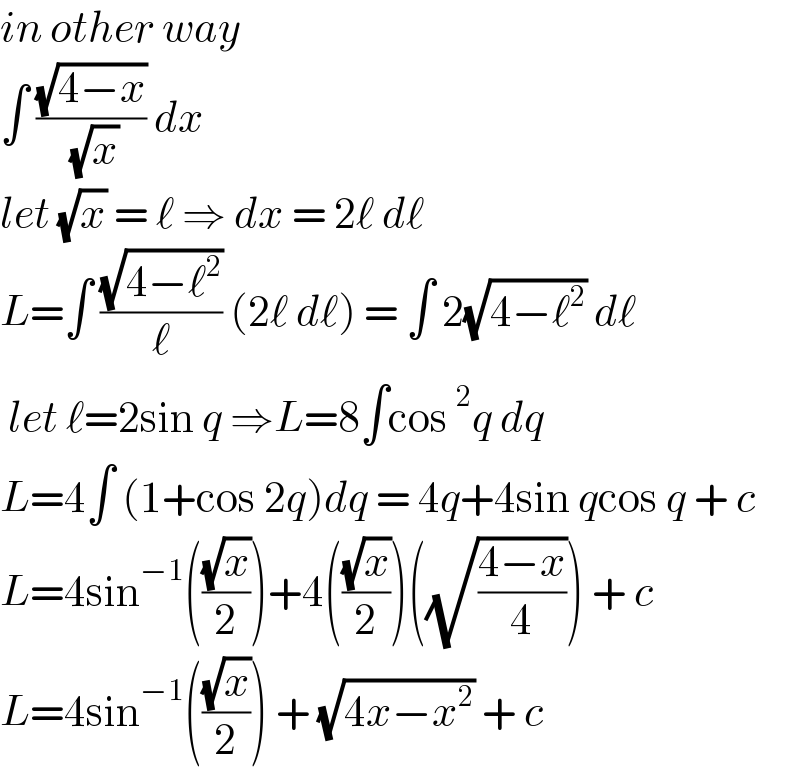
in other way ∫ ((√(4−x))/( (√x))) dx let (√x) = ℓ ⇒ dx = 2ℓ dℓ L=∫ ((√(4−ℓ^2 ))/ℓ) (2ℓ dℓ) = ∫ 2(√(4−ℓ^2 )) dℓ let ℓ=2sin q ⇒L=8∫cos^2 q dq L=4∫ (1+cos 2q)dq = 4q+4sin qcos q + c L=4sin^(−1) (((√x)/2))+4(((√x)/2))((√((4−x)/4))) + c L=4sin^(−1) (((√x)/2)) + (√(4x−x^2 )) + c
$${in}\:{other}\:{way}\: \\ $$$$\int\:\frac{\sqrt{\mathrm{4}−{x}}}{\:\sqrt{{x}}}\:{dx}\: \\ $$$${let}\:\sqrt{{x}}\:=\:\ell\:\Rightarrow\:{dx}\:=\:\mathrm{2}\ell\:{d}\ell \\ $$$${L}=\int\:\frac{\sqrt{\mathrm{4}−\ell^{\mathrm{2}} }}{\ell}\:\left(\mathrm{2}\ell\:{d}\ell\right)\:=\:\int\:\mathrm{2}\sqrt{\mathrm{4}−\ell^{\mathrm{2}} }\:{d}\ell \\ $$$$\:{let}\:\ell=\mathrm{2sin}\:{q}\:\Rightarrow{L}=\mathrm{8}\int\mathrm{cos}\:^{\mathrm{2}} {q}\:{dq} \\ $$$${L}=\mathrm{4}\int\:\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}{q}\right){dq}\:=\:\mathrm{4}{q}+\mathrm{4sin}\:{q}\mathrm{cos}\:{q}\:+\:{c} \\ $$$${L}=\mathrm{4sin}^{−\mathrm{1}} \left(\frac{\sqrt{{x}}}{\mathrm{2}}\right)+\mathrm{4}\left(\frac{\sqrt{{x}}}{\mathrm{2}}\right)\left(\sqrt{\frac{\mathrm{4}−{x}}{\mathrm{4}}}\right)\:+\:{c} \\ $$$${L}=\mathrm{4sin}^{−\mathrm{1}} \left(\frac{\sqrt{{x}}}{\mathrm{2}}\right)\:+\:\sqrt{\mathrm{4}{x}−{x}^{\mathrm{2}} }\:+\:{c}\: \\ $$
Answered by liberty last updated on 28/Dec/20
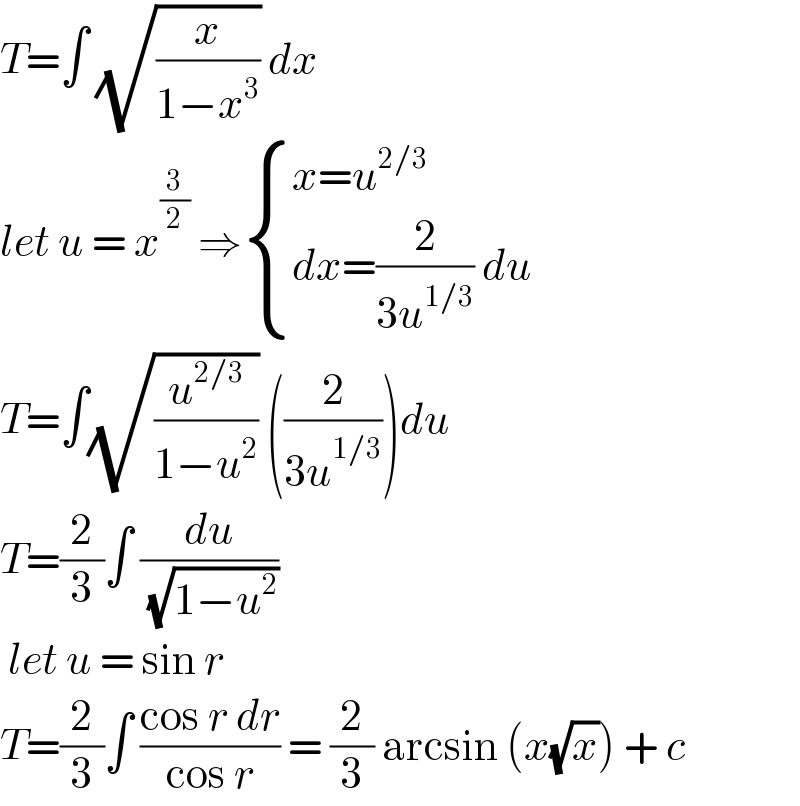
T=∫ (√(x/(1−x^3 ))) dx let u = x^(3/2) ⇒ { ((x=u^(2/3) )),((dx=(2/(3u^(1/3) )) du)) :} T=∫(√(u^(2/3) /(1−u^2 ))) ((2/(3u^(1/3) )))du T=(2/3)∫ (du/( (√(1−u^2 )))) let u = sin r T=(2/3)∫ ((cos r dr)/(cos r)) = (2/3) arcsin (x(√x)) + c
$${T}=\int\:\sqrt{\frac{{x}}{\mathrm{1}−{x}^{\mathrm{3}} }}\:{dx}\: \\ $$$${let}\:{u}\:=\:{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \:\Rightarrow\begin{cases}{{x}={u}^{\mathrm{2}/\mathrm{3}} }\\{{dx}=\frac{\mathrm{2}}{\mathrm{3}{u}^{\mathrm{1}/\mathrm{3}} }\:{du}}\end{cases} \\ $$$${T}=\int\sqrt{\frac{{u}^{\mathrm{2}/\mathrm{3}} }{\mathrm{1}−{u}^{\mathrm{2}} }}\:\left(\frac{\mathrm{2}}{\mathrm{3}{u}^{\mathrm{1}/\mathrm{3}} }\right){du} \\ $$$${T}=\frac{\mathrm{2}}{\mathrm{3}}\int\:\frac{{du}}{\:\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }}\: \\ $$$$\:{let}\:{u}\:=\:\mathrm{sin}\:{r}\: \\ $$$${T}=\frac{\mathrm{2}}{\mathrm{3}}\int\:\frac{\mathrm{cos}\:{r}\:{dr}}{\mathrm{cos}\:{r}}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{arcsin}\:\left({x}\sqrt{{x}}\right)\:+\:{c}\: \\ $$
Commented by liberty last updated on 28/Dec/20
problema integrali tajba, teħtieġ il-kunċett ta 'trigonometrija u integrali bażiċi
Answered by liberty last updated on 28/Dec/20
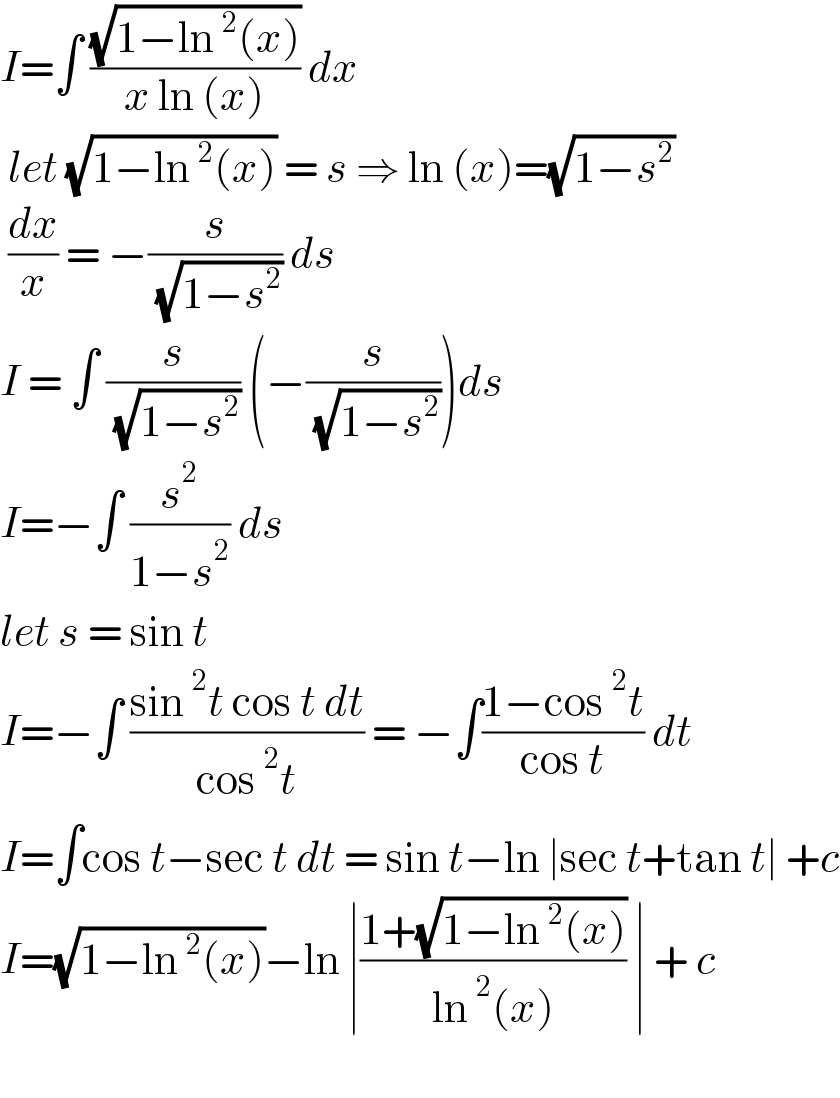
I=∫ ((√(1−ln^2 (x)))/(x ln (x))) dx let (√(1−ln^2 (x))) = s ⇒ ln (x)=(√(1−s^2 )) (dx/x) = −(s/( (√(1−s^2 )))) ds I = ∫ (s/( (√(1−s^2 )))) (−(s/( (√(1−s^2 )))))ds I=−∫ (s^2 /(1−s^2 )) ds let s = sin t I=−∫ ((sin^2 t cos t dt)/(cos^2 t)) = −∫((1−cos^2 t)/(cos t)) dt I=∫cos t−sec t dt = sin t−ln ∣sec t+tan t∣ +c I=(√(1−ln^2 (x)))−ln ∣((1+(√(1−ln^2 (x))))/(ln^2 (x))) ∣ + c
$${I}=\int\:\frac{\sqrt{\mathrm{1}−\mathrm{ln}\:^{\mathrm{2}} \left({x}\right)}}{{x}\:\mathrm{ln}\:\left({x}\right)}\:{dx} \\ $$$$\:{let}\:\sqrt{\mathrm{1}−\mathrm{ln}\:^{\mathrm{2}} \left({x}\right)}\:=\:{s}\:\Rightarrow\:\mathrm{ln}\:\left({x}\right)=\sqrt{\mathrm{1}−{s}^{\mathrm{2}} }\: \\ $$$$\:\frac{{dx}}{{x}}\:=\:−\frac{{s}}{\:\sqrt{\mathrm{1}−{s}^{\mathrm{2}} }}\:{ds}\: \\ $$$${I}\:=\:\int\:\frac{{s}}{\:\sqrt{\mathrm{1}−{s}^{\mathrm{2}} }}\:\left(−\frac{{s}}{\:\sqrt{\mathrm{1}−{s}^{\mathrm{2}} }}\right){ds}\: \\ $$$${I}=−\int\:\frac{{s}^{\mathrm{2}} }{\mathrm{1}−{s}^{\mathrm{2}} }\:{ds}\: \\ $$$${let}\:{s}\:=\:\mathrm{sin}\:{t}\: \\ $$$${I}=−\int\:\frac{\mathrm{sin}\:^{\mathrm{2}} {t}\:\mathrm{cos}\:{t}\:{dt}}{\mathrm{cos}\:^{\mathrm{2}} {t}}\:=\:−\int\frac{\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {t}}{\mathrm{cos}\:{t}}\:{dt}\: \\ $$$${I}=\int\mathrm{cos}\:{t}−\mathrm{sec}\:{t}\:{dt}\:=\:\mathrm{sin}\:{t}−\mathrm{ln}\:\mid\mathrm{sec}\:{t}+\mathrm{tan}\:{t}\mid\:+{c} \\ $$$${I}=\sqrt{\mathrm{1}−\mathrm{ln}\:^{\mathrm{2}} \left({x}\right)}−\mathrm{ln}\:\mid\frac{\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{ln}\:^{\mathrm{2}} \left({x}\right)}}{\mathrm{ln}\:^{\mathrm{2}} \left({x}\right)}\:\mid\:+\:{c}\: \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 28/Dec/20
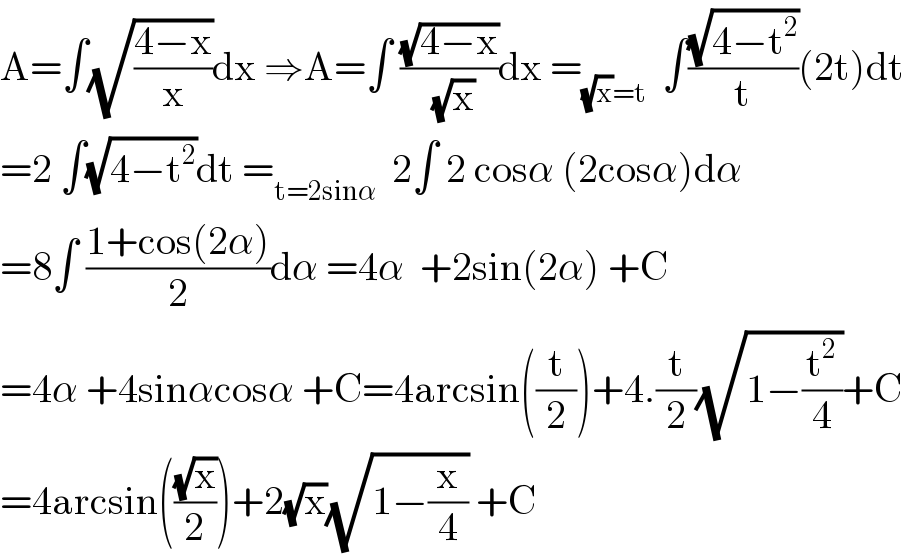
A=∫(√((4−x)/x))dx ⇒A=∫ ((√(4−x))/( (√x)))dx =_((√x)=t) ∫((√(4−t^2 ))/t)(2t)dt =2 ∫(√(4−t^2 ))dt =_(t=2sinα) 2∫ 2 cosα (2cosα)dα =8∫ ((1+cos(2α))/2)dα =4α +2sin(2α) +C =4α +4sinαcosα +C=4arcsin((t/2))+4.(t/2)(√(1−(t^2 /4)))+C =4arcsin(((√x)/2))+2(√x)(√(1−(x/4))) +C
$$\mathrm{A}=\int\sqrt{\frac{\mathrm{4}−\mathrm{x}}{\mathrm{x}}}\mathrm{dx}\:\Rightarrow\mathrm{A}=\int\:\frac{\sqrt{\mathrm{4}−\mathrm{x}}}{\:\sqrt{\mathrm{x}}}\mathrm{dx}\:=_{\sqrt{\mathrm{x}}=\mathrm{t}} \:\:\int\frac{\sqrt{\mathrm{4}−\mathrm{t}^{\mathrm{2}} }}{\mathrm{t}}\left(\mathrm{2t}\right)\mathrm{dt} \\ $$$$=\mathrm{2}\:\int\sqrt{\mathrm{4}−\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:=_{\mathrm{t}=\mathrm{2sin}\alpha} \:\:\mathrm{2}\int\:\mathrm{2}\:\mathrm{cos}\alpha\:\left(\mathrm{2cos}\alpha\right)\mathrm{d}\alpha \\ $$$$=\mathrm{8}\int\:\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2}\alpha\right)}{\mathrm{2}}\mathrm{d}\alpha\:=\mathrm{4}\alpha\:\:+\mathrm{2sin}\left(\mathrm{2}\alpha\right)\:+\mathrm{C} \\ $$$$=\mathrm{4}\alpha\:+\mathrm{4sin}\alpha\mathrm{cos}\alpha\:+\mathrm{C}=\mathrm{4arcsin}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)+\mathrm{4}.\frac{\mathrm{t}}{\mathrm{2}}\sqrt{\mathrm{1}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{4}}}+\mathrm{C} \\ $$$$=\mathrm{4arcsin}\left(\frac{\sqrt{\mathrm{x}}}{\mathrm{2}}\right)+\mathrm{2}\sqrt{\mathrm{x}}\sqrt{\mathrm{1}−\frac{\mathrm{x}}{\mathrm{4}}}\:+\mathrm{C} \\ $$
Answered by mathmax by abdo last updated on 29/Dec/20
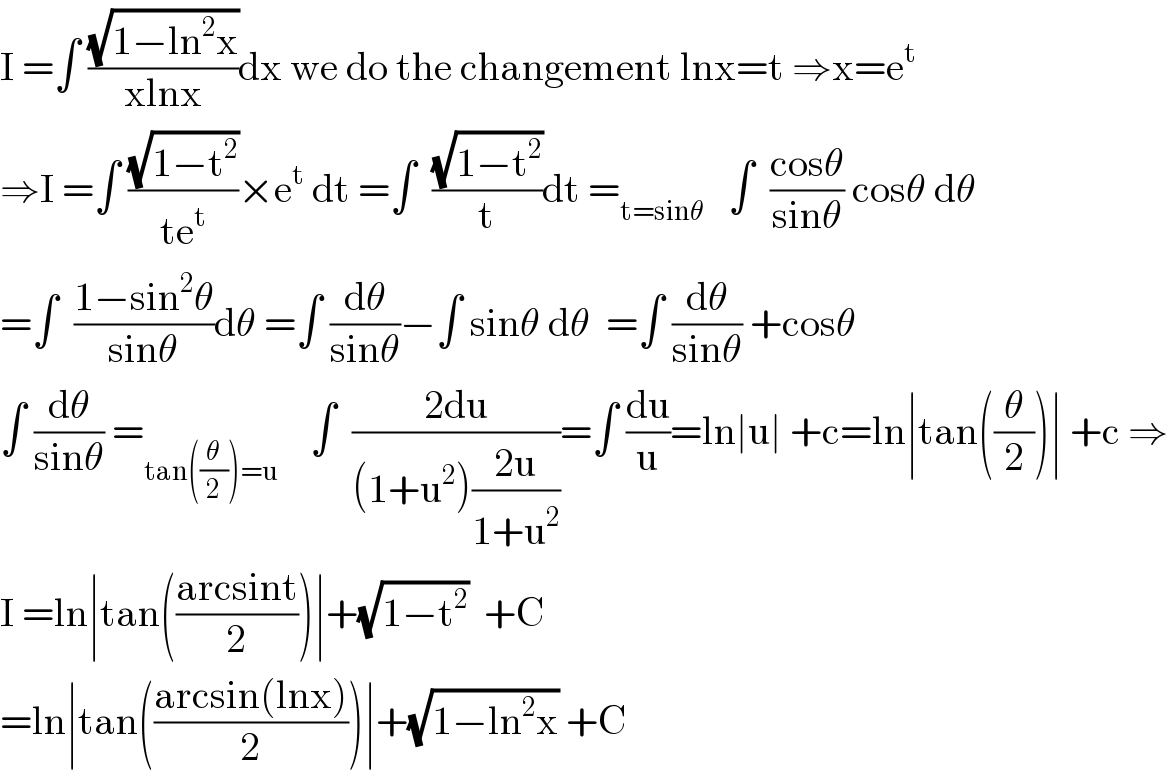
I =∫ ((√(1−ln^2 x))/(xlnx))dx we do the changement lnx=t ⇒x=e^t ⇒I =∫ ((√(1−t^2 ))/(te^t ))×e^t dt =∫ ((√(1−t^2 ))/t)dt =_(t=sinθ) ∫ ((cosθ)/(sinθ)) cosθ dθ =∫ ((1−sin^2 θ)/(sinθ))dθ =∫ (dθ/(sinθ))−∫ sinθ dθ =∫ (dθ/(sinθ)) +cosθ ∫ (dθ/(sinθ)) =_(tan((θ/2))=u) ∫ ((2du)/((1+u^2 )((2u)/(1+u^2 ))))=∫ (du/u)=ln∣u∣ +c=ln∣tan((θ/2))∣ +c ⇒ I =ln∣tan(((arcsint)/2))∣+(√(1−t^2 )) +C =ln∣tan(((arcsin(lnx))/2))∣+(√(1−ln^2 x)) +C
$$\mathrm{I}\:=\int\:\frac{\sqrt{\mathrm{1}−\mathrm{ln}^{\mathrm{2}} \mathrm{x}}}{\mathrm{xlnx}}\mathrm{dx}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{lnx}=\mathrm{t}\:\Rightarrow\mathrm{x}=\mathrm{e}^{\mathrm{t}} \\ $$$$\Rightarrow\mathrm{I}\:=\int\:\frac{\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }}{\mathrm{te}^{\mathrm{t}} }×\mathrm{e}^{\mathrm{t}} \:\mathrm{dt}\:=\int\:\:\frac{\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }}{\mathrm{t}}\mathrm{dt}\:=_{\mathrm{t}=\mathrm{sin}\theta} \:\:\:\int\:\:\frac{\mathrm{cos}\theta}{\mathrm{sin}\theta}\:\mathrm{cos}\theta\:\mathrm{d}\theta \\ $$$$=\int\:\:\frac{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta}{\mathrm{sin}\theta}\mathrm{d}\theta\:=\int\:\frac{\mathrm{d}\theta}{\mathrm{sin}\theta}−\int\:\mathrm{sin}\theta\:\mathrm{d}\theta\:\:=\int\:\frac{\mathrm{d}\theta}{\mathrm{sin}\theta}\:+\mathrm{cos}\theta \\ $$$$\int\:\frac{\mathrm{d}\theta}{\mathrm{sin}\theta}\:=_{\mathrm{tan}\left(\frac{\theta}{\mathrm{2}}\right)=\mathrm{u}} \:\:\:\:\int\:\:\frac{\mathrm{2du}}{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\frac{\mathrm{2u}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }}=\int\:\frac{\mathrm{du}}{\mathrm{u}}=\mathrm{ln}\mid\mathrm{u}\mid\:+\mathrm{c}=\mathrm{ln}\mid\mathrm{tan}\left(\frac{\theta}{\mathrm{2}}\right)\mid\:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{I}\:=\mathrm{ln}\mid\mathrm{tan}\left(\frac{\mathrm{arcsint}}{\mathrm{2}}\right)\mid+\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\:\:+\mathrm{C} \\ $$$$=\mathrm{ln}\mid\mathrm{tan}\left(\frac{\mathrm{arcsin}\left(\mathrm{lnx}\right)}{\mathrm{2}}\right)\mid+\sqrt{\mathrm{1}−\mathrm{ln}^{\mathrm{2}} \mathrm{x}}\:+\mathrm{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *