nice-calculus-0-pi-2-x-3-cot-x-dx-a-16-a-m-n-

Question Number 151954 by mnjuly1970 last updated on 24/Aug/21

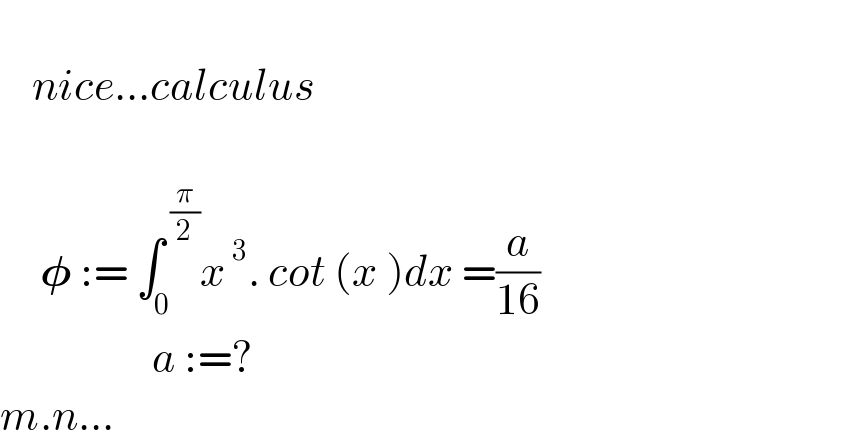
nice...calculus 𝛗 := ∫_0 ^( (π/2)) x^( 3) . cot (x )dx =(a/(16)) a :=? m.n...

$$ \\ $$$$\:\:\:\:{nice}…{calculus} \\ $$$$\: \\ $$$$\:\:\:\:\:\boldsymbol{\phi}\::=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {x}^{\:\mathrm{3}} .\:{cot}\:\left({x}\:\right){dx}\:=\frac{{a}}{\mathrm{16}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}\::=? \\ $$$${m}.{n}… \\ $$

Answered by Kamel last updated on 24/Aug/21

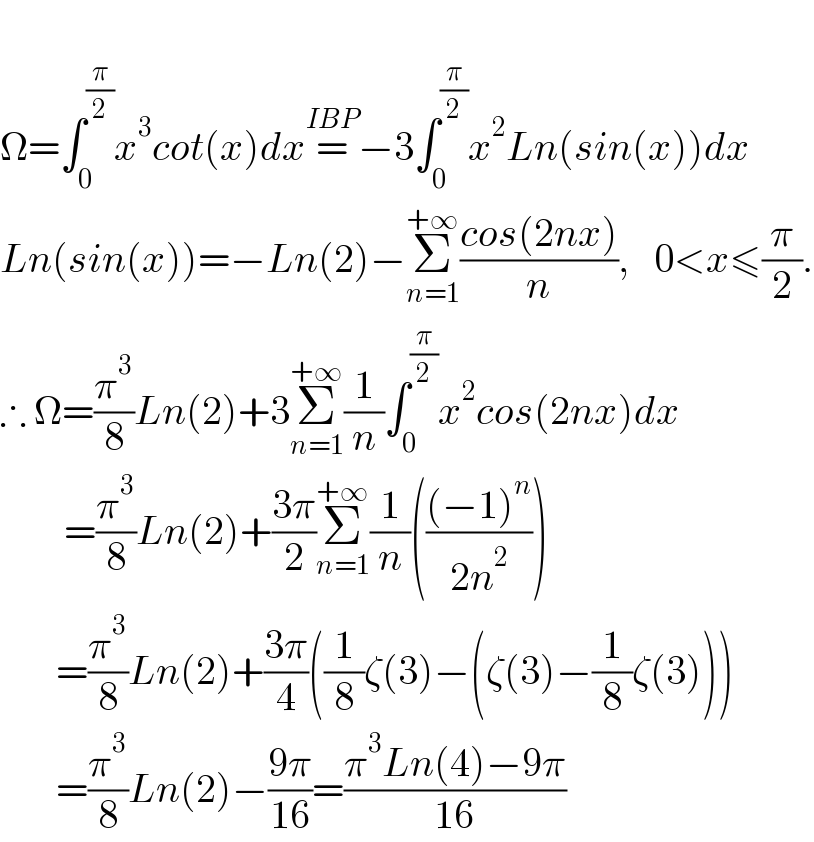
Ω=∫_0 ^(π/2) x^3 cot(x)dx=^(IBP) −3∫_0 ^(π/2) x^2 Ln(sin(x))dx Ln(sin(x))=−Ln(2)−Σ_(n=1) ^(+∞) ((cos(2nx))/n), 0<x≤(π/2). ∴ Ω=(π^3 /8)Ln(2)+3Σ_(n=1) ^(+∞) (1/n)∫_0 ^(π/2) x^2 cos(2nx)dx =(π^3 /8)Ln(2)+((3π)/2)Σ_(n=1) ^(+∞) (1/n)((((−1)^n )/(2n^2 ))) =(π^3 /8)Ln(2)+((3π)/4)((1/8)ζ(3)−(ζ(3)−(1/8)ζ(3))) =(π^3 /8)Ln(2)−((9π)/(16))=((π^3 Ln(4)−9π)/(16))

$$ \\ $$$$\Omega=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {x}^{\mathrm{3}} {cot}\left({x}\right){dx}\overset{{IBP}} {=}−\mathrm{3}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {x}^{\mathrm{2}} {Ln}\left({sin}\left({x}\right)\right){dx} \\ $$$${Ln}\left({sin}\left({x}\right)\right)=−{Ln}\left(\mathrm{2}\right)−\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{{cos}\left(\mathrm{2}{nx}\right)}{{n}},\:\:\:\mathrm{0}<{x}\leqslant\frac{\pi}{\mathrm{2}}. \\ $$$$\therefore\:\Omega=\frac{\pi^{\mathrm{3}} }{\mathrm{8}}{Ln}\left(\mathrm{2}\right)+\mathrm{3}\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {x}^{\mathrm{2}} {cos}\left(\mathrm{2}{nx}\right){dx} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\pi^{\mathrm{3}} }{\mathrm{8}}{Ln}\left(\mathrm{2}\right)+\frac{\mathrm{3}\pi}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{{n}}\left(\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:\:\:\:=\frac{\pi^{\mathrm{3}} }{\mathrm{8}}{Ln}\left(\mathrm{2}\right)+\frac{\mathrm{3}\pi}{\mathrm{4}}\left(\frac{\mathrm{1}}{\mathrm{8}}\zeta\left(\mathrm{3}\right)−\left(\zeta\left(\mathrm{3}\right)−\frac{\mathrm{1}}{\mathrm{8}}\zeta\left(\mathrm{3}\right)\right)\right) \\ $$$$\:\:\:\:\:\:\:=\frac{\pi^{\mathrm{3}} }{\mathrm{8}}{Ln}\left(\mathrm{2}\right)−\frac{\mathrm{9}\pi}{\mathrm{16}}=\frac{\pi^{\mathrm{3}} {Ln}\left(\mathrm{4}\right)−\mathrm{9}\pi}{\mathrm{16}} \\ $$

Commented by mnjuly1970 last updated on 25/Aug/21

$${excellent}… \\ $$

Facebook Tweet Pin

nice-calculus-0-pi-2-x-3-cot-x-dx-a-16-a-m-n-

Leave a Reply Cancel reply