Question Number 128797 by mnjuly1970 last updated on 10/Jan/21
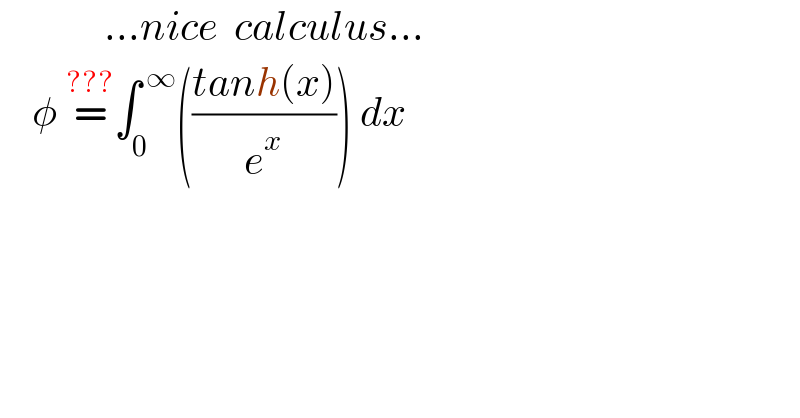
$$\:\:\:\:\:\:\:\:\:\:\:\:\:…{nice}\:\:{calculus}… \\ $$$$\:\:\:\:\phi\:\overset{???} {=}\int_{\mathrm{0}} ^{\:\infty} \left(\frac{{tanh}\left({x}\right)}{{e}^{{x}} }\right)\:{dx} \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 10/Jan/21
![∫_0 ^∞ ((tanh(x))/e^x )dx=∫_0 ^∞ ((e^(2x) −1)/(e^(2x) +1)).(1/e^x )dx=∫_0 ^∞ e^(−x) dx−2∫_0 ^∞ (1/(e^x (e^(2x) +1)))dx =1−2∫_1 ^∞ (1/t^2 )−(1/(t^2 +1))dt e^x =t =1−2+[2(tan^(−1) t)]_1 ^∞ =(π/2)−1](https://www.tinkutara.com/question/Q128800.png)
$$\int_{\mathrm{0}} ^{\infty} \frac{{tanh}\left({x}\right)}{{e}^{{x}} }{dx}=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{\mathrm{2}{x}} −\mathrm{1}}{{e}^{\mathrm{2}{x}} +\mathrm{1}}.\frac{\mathrm{1}}{{e}^{{x}} }{dx}=\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} {dx}−\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{e}^{{x}} \left({e}^{\mathrm{2}{x}} +\mathrm{1}\right)}{dx} \\ $$$$=\mathrm{1}−\mathrm{2}\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}\:\:\:\:\:\:{e}^{{x}} ={t} \\ $$$$=\mathrm{1}−\mathrm{2}+\left[\mathrm{2}\left({tan}^{−\mathrm{1}} {t}\right)\right]_{\mathrm{1}} ^{\infty} =\frac{\pi}{\mathrm{2}}−\mathrm{1} \\ $$
Commented by mnjuly1970 last updated on 10/Jan/21

$$\:\:{thanks}\:{alot}… \\ $$
Answered by Olaf last updated on 10/Jan/21
![...nice calculus... φ =^(???) ∫_0 ^( ∞) (((tanh(x))/e^x )) dx φ = ∫_0 ^∞ ((tanhx)/e^x )dx Let u = e^x φ = ∫_1 ^∞ (((u−(1/u))/(u+(1/u)))/u).(du/u) φ = ∫_1 ^∞ ((u^2 −1)/(u^2 (u^2 +1)))du φ = ∫_1 ^∞ [(2/(1+u^2 ))−(1/u^2 )]du φ = [2arctanu+(1/u)]_1 ^∞ φ =( 2(π/2)+0)−(2(π/4)+1) = (π/2)−1](https://www.tinkutara.com/question/Q128810.png)
$$\:\:\:\:\:\:\:\:\:\:\:\:\:…{nice}\:\:{calculus}… \\ $$$$\:\:\:\:\phi\:\overset{???} {=}\int_{\mathrm{0}} ^{\:\infty} \left(\frac{{tanh}\left({x}\right)}{{e}^{{x}} }\right)\:{dx} \\ $$$$\phi\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{tanh}{x}}{{e}^{{x}} }{dx} \\ $$$$\mathrm{Let}\:{u}\:=\:{e}^{{x}} \\ $$$$\phi\:=\:\int_{\mathrm{1}} ^{\infty} \frac{\frac{{u}−\frac{\mathrm{1}}{{u}}}{{u}+\frac{\mathrm{1}}{{u}}}}{{u}}.\frac{{du}}{{u}} \\ $$$$\phi\:=\:\int_{\mathrm{1}} ^{\infty} \frac{{u}^{\mathrm{2}} −\mathrm{1}}{{u}^{\mathrm{2}} \left({u}^{\mathrm{2}} +\mathrm{1}\right)}{du} \\ $$$$\phi\:=\:\int_{\mathrm{1}} ^{\infty} \left[\frac{\mathrm{2}}{\mathrm{1}+{u}^{\mathrm{2}} }−\frac{\mathrm{1}}{{u}^{\mathrm{2}} }\right]{du} \\ $$$$\phi\:=\:\left[\mathrm{2arctan}{u}+\frac{\mathrm{1}}{{u}}\right]_{\mathrm{1}} ^{\infty} \\ $$$$\phi\:=\left(\:\mathrm{2}\frac{\pi}{\mathrm{2}}+\mathrm{0}\right)−\left(\mathrm{2}\frac{\pi}{\mathrm{4}}+\mathrm{1}\right)\:=\:\frac{\pi}{\mathrm{2}}−\mathrm{1} \\ $$
Commented by mnjuly1970 last updated on 10/Jan/21
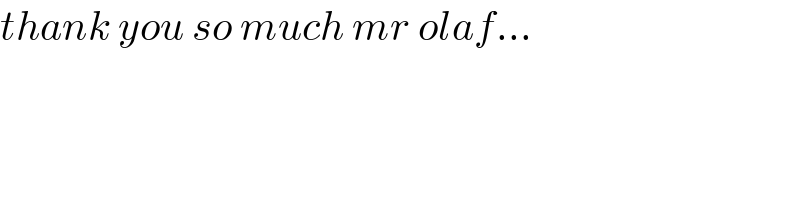
$${thank}\:{you}\:{so}\:{much}\:{mr}\:{olaf}… \\ $$
