Question Number 122290 by mnjuly1970 last updated on 15/Nov/20
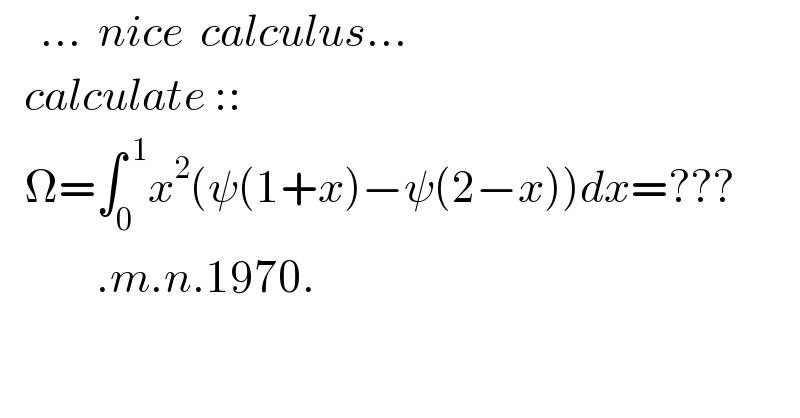
$$\:\:\:\:\:…\:\:{nice}\:\:{calculus}… \\ $$$$\:\:\:{calculate}\::: \\ $$$$\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\mathrm{1}} {x}^{\mathrm{2}} \left(\psi\left(\mathrm{1}+{x}\right)−\psi\left(\mathrm{2}−{x}\right)\right){dx}=??? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:.{m}.{n}.\mathrm{1970}. \\ $$
Commented by Dwaipayan Shikari last updated on 15/Nov/20

$$\mathrm{2}−{log}\left(\mathrm{2}\pi\right) \\ $$
Answered by mnjuly1970 last updated on 16/Nov/20
![solution: Φ=∫_0 ^( 1) x^2 ψ(2−x)dx=^(∫_a ^( b) f(x)=∫_a ^( b) f(a+b−x)dx) ∫_0 ^( 1) (1−x)^2 ψ(1+x)dx ∴ Ω=∫_0 ^( 1) x^2 (ψ(1+x))dx−∫_0 ^( 1) (1−x)^2 ψ(1+x)dx =∫_0 ^( 1) (2x−1)ψ(1+x)dx=[(2x−1)lnΓ(x+1)]_0 ^1 −2∫_0 ^( 1) lnΓ(x+1)dx =−2∫_0 ^( 1) ln(x)−2∫_0 ^( 1) ln(Γ(x))dx =2−2((1/2)ln(2π))=2−ln(2π) ✓ ..m.n..](https://www.tinkutara.com/question/Q122389.png)
$$\:\:\:{solution}: \\ $$$$\:\:\:\:\:\:\Phi=\int_{\mathrm{0}} ^{\:\mathrm{1}} {x}^{\mathrm{2}} \psi\left(\mathrm{2}−{x}\right){dx}\overset{\int_{{a}} ^{\:{b}} {f}\left({x}\right)=\int_{{a}} ^{\:{b}} {f}\left({a}+{b}−{x}\right){dx}} {=}\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\mathrm{1}−{x}\right)^{\mathrm{2}} \psi\left(\mathrm{1}+{x}\right){dx} \\ $$$$\therefore\:\Omega=\int_{\mathrm{0}} ^{\:\mathrm{1}} {x}^{\mathrm{2}} \left(\psi\left(\mathrm{1}+{x}\right)\right){dx}−\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\mathrm{1}−{x}\right)^{\mathrm{2}} \psi\left(\mathrm{1}+{x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\mathrm{2}{x}−\mathrm{1}\right)\psi\left(\mathrm{1}+{x}\right){dx}=\left[\left(\mathrm{2}{x}−\mathrm{1}\right){ln}\Gamma\left({x}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\Gamma\left({x}+\mathrm{1}\right){dx} \\ $$$$=−\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\left({x}\right)−\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\left(\Gamma\left({x}\right)\right){dx} \\ $$$$=\mathrm{2}−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\pi\right)\right)=\mathrm{2}−{ln}\left(\mathrm{2}\pi\right)\:\:\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:..{m}.{n}.. \\ $$
