Question Number 127649 by mnjuly1970 last updated on 31/Dec/20
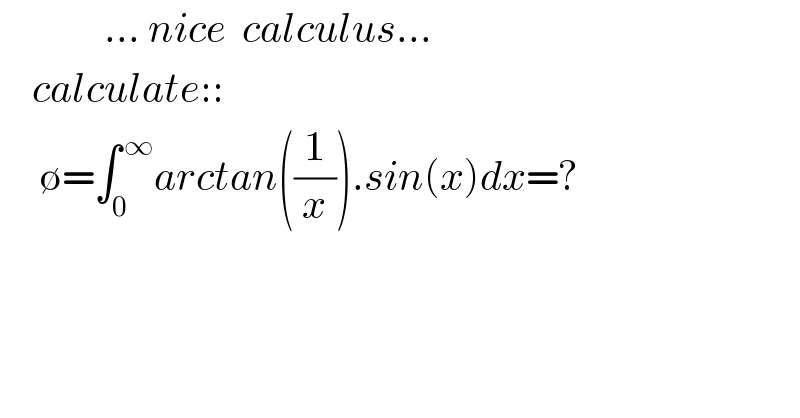
$$\:\:\:\:\:\:\:\:\:\:\:\:\:…\:{nice}\:\:{calculus}… \\ $$$$\:\:\:\:{calculate}:: \\ $$$$\:\:\:\:\:\emptyset=\int_{\mathrm{0}} ^{\:\infty} {arctan}\left(\frac{\mathrm{1}}{{x}}\right).{sin}\left({x}\right){dx}=? \\ $$$$ \\ $$
Answered by mindispower last updated on 31/Dec/20
![f(t)=∫_0 ^∞ arctan((t/x))sin(x)dx t∈]0,1] f(0)=0 f′(t)=∫_0 ^∞ ((xsin(x))/(x^2 +t^2 ))dx let f(z)=((zsin(z))/(z^2 +t^2 )),Im(z)>0 pol(f)=z∈{it} ∫_(−∞) ^∞ f(z)dz=2∫_0 ^∞ f(z)dz= ∫_(−∞) ^∞ f(z)dz=Im∫_(−∞) ^∞ ((ze^(iz) )/(z^2 +t^2 ))dz=Im(2iπRes(((ze^(iz) )/(z^2 +t^2 ))),z=it} =Im(2iπ((ite^(−t) )/(2it)))=πe^(−t) f′(t)=(π/2)e^(−t) f(t)=−((πe^(−t) )/2)+c f(0)=0⇒c=(π/2) f(t)=(π/2)(1−e^(−t) ) ∅=f(1)=πe^(−(1/2)) (((e^(1/2) −e^(−(1/2)) )/2))=((πsh((1/2)))/( (√e)))≈0.9923](https://www.tinkutara.com/question/Q127661.png)
$${f}\left({t}\right)=\int_{\mathrm{0}} ^{\infty} {arctan}\left(\frac{{t}}{{x}}\right){sin}\left({x}\right){dx} \\ $$$$\left.{t}\left.\in\right]\mathrm{0},\mathrm{1}\right] \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${f}'\left({t}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{xsin}\left({x}\right)}{{x}^{\mathrm{2}} +{t}^{\mathrm{2}} }{dx} \\ $$$${let}\:{f}\left({z}\right)=\frac{{zsin}\left({z}\right)}{{z}^{\mathrm{2}} +{t}^{\mathrm{2}} },{Im}\left({z}\right)>\mathrm{0} \\ $$$${pol}\left({f}\right)={z}\in\left\{{it}\right\} \\ $$$$\int_{−\infty} ^{\infty} {f}\left({z}\right){dz}=\mathrm{2}\int_{\mathrm{0}} ^{\infty} {f}\left({z}\right){dz}= \\ $$$$\int_{−\infty} ^{\infty} {f}\left({z}\right){dz}={Im}\int_{−\infty} ^{\infty} \frac{{ze}^{{iz}} }{{z}^{\mathrm{2}} +{t}^{\mathrm{2}} }{dz}={Im}\left(\mathrm{2}{i}\pi{Res}\left(\frac{{ze}^{{iz}} }{{z}^{\mathrm{2}} +{t}^{\mathrm{2}} }\right),{z}={it}\right\} \\ $$$$={Im}\left(\mathrm{2}{i}\pi\frac{{ite}^{−{t}} }{\mathrm{2}{it}}\right)=\pi{e}^{−{t}} \\ $$$${f}'\left({t}\right)=\frac{\pi}{\mathrm{2}}{e}^{−{t}} \\ $$$${f}\left({t}\right)=−\frac{\pi{e}^{−{t}} }{\mathrm{2}}+{c} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0}\Rightarrow{c}=\frac{\pi}{\mathrm{2}} \\ $$$${f}\left({t}\right)=\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−{e}^{−{t}} \right) \\ $$$$\emptyset={f}\left(\mathrm{1}\right)=\pi{e}^{−\frac{\mathrm{1}}{\mathrm{2}}} \left(\frac{{e}^{\frac{\mathrm{1}}{\mathrm{2}}} −{e}^{−\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{2}}\right)=\frac{\pi{sh}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\:\sqrt{{e}}}\approx\mathrm{0}.\mathrm{9923} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 31/Dec/20
![]thak you sir power extraorinary..as always...](https://www.tinkutara.com/question/Q127667.png)
$$\left.\right]{thak}\:{you}\:{sir}\:{power} \\ $$$${extraorinary}..{as}\:{always}… \\ $$
Answered by mathmax by abdo last updated on 01/Jan/21
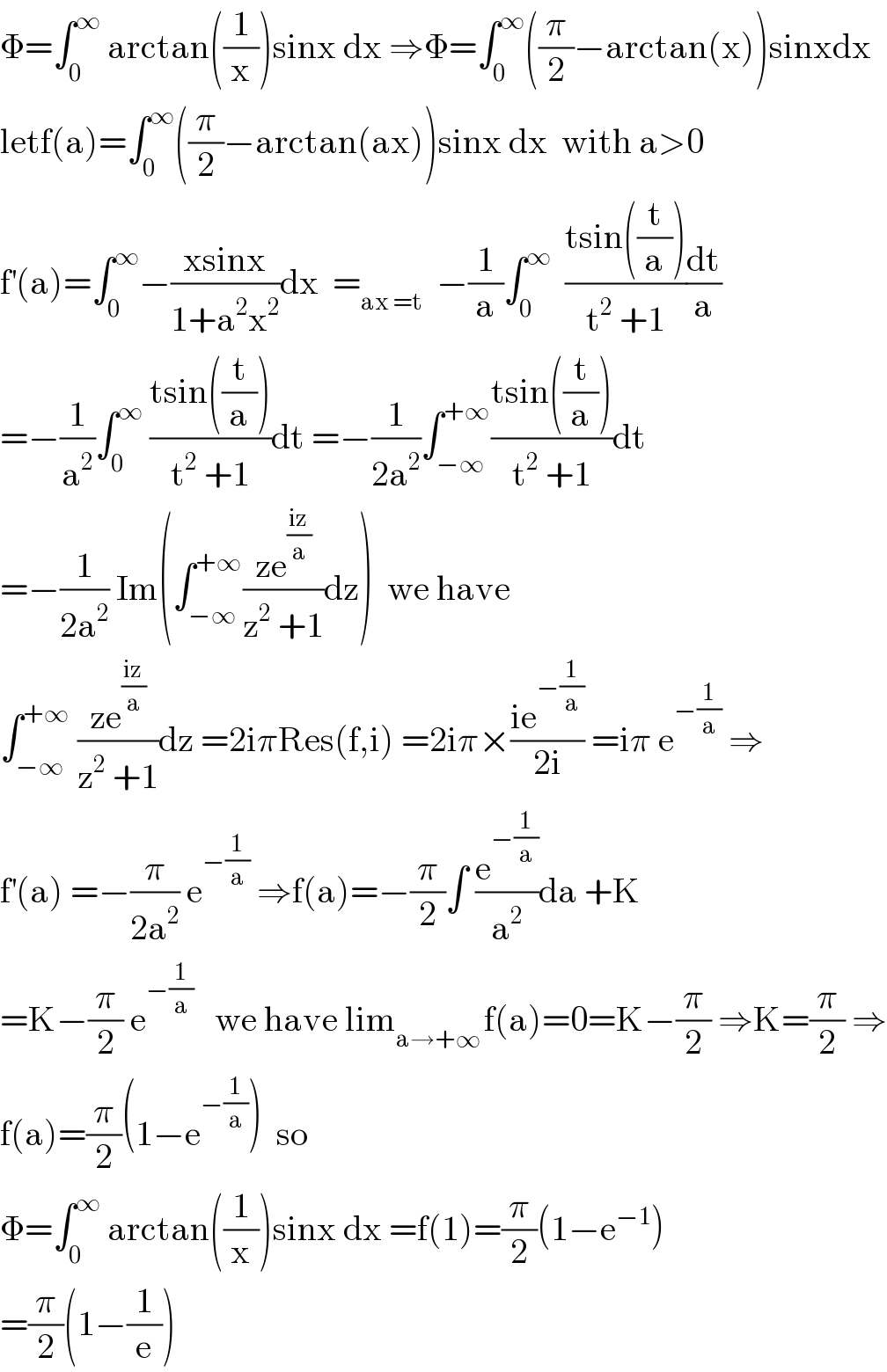
$$\Phi=\int_{\mathrm{0}} ^{\infty} \:\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\mathrm{sinx}\:\mathrm{dx}\:\Rightarrow\Phi=\int_{\mathrm{0}} ^{\infty} \left(\frac{\pi}{\mathrm{2}}−\mathrm{arctan}\left(\mathrm{x}\right)\right)\mathrm{sinxdx} \\ $$$$\mathrm{letf}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \left(\frac{\pi}{\mathrm{2}}−\mathrm{arctan}\left(\mathrm{ax}\right)\right)\mathrm{sinx}\:\mathrm{dx}\:\:\mathrm{with}\:\mathrm{a}>\mathrm{0} \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} −\frac{\mathrm{xsinx}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\:=_{\mathrm{ax}\:=\mathrm{t}} \:\:−\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{tsin}\left(\frac{\mathrm{t}}{\mathrm{a}}\right)}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\frac{\mathrm{dt}}{\mathrm{a}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{tsin}\left(\frac{\mathrm{t}}{\mathrm{a}}\right)}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\:=−\frac{\mathrm{1}}{\mathrm{2a}^{\mathrm{2}} }\int_{−\infty} ^{+\infty} \frac{\mathrm{tsin}\left(\frac{\mathrm{t}}{\mathrm{a}}\right)}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2a}^{\mathrm{2}} }\:\mathrm{Im}\left(\int_{−\infty} ^{+\infty} \frac{\mathrm{ze}^{\frac{\mathrm{iz}}{\mathrm{a}}} }{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dz}\right)\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{−\infty} ^{+\infty} \:\frac{\mathrm{ze}^{\frac{\mathrm{iz}}{\mathrm{a}}} }{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dz}\:=\mathrm{2i}\pi\mathrm{Res}\left(\mathrm{f},\mathrm{i}\right)\:=\mathrm{2i}\pi×\frac{\mathrm{ie}^{−\frac{\mathrm{1}}{\mathrm{a}}} }{\mathrm{2i}}\:=\mathrm{i}\pi\:\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{a}}} \:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)\:=−\frac{\pi}{\mathrm{2a}^{\mathrm{2}} }\:\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{a}}} \:\Rightarrow\mathrm{f}\left(\mathrm{a}\right)=−\frac{\pi}{\mathrm{2}}\int\:\frac{\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{a}}} }{\mathrm{a}^{\mathrm{2}} }\mathrm{da}\:+\mathrm{K} \\ $$$$=\mathrm{K}−\frac{\pi}{\mathrm{2}}\:\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{a}}} \:\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{lim}_{\mathrm{a}\rightarrow+\infty\:} \mathrm{f}\left(\mathrm{a}\right)=\mathrm{0}=\mathrm{K}−\frac{\pi}{\mathrm{2}}\:\Rightarrow\mathrm{K}=\frac{\pi}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{a}}} \right)\:\:\mathrm{so} \\ $$$$\Phi=\int_{\mathrm{0}} ^{\infty} \:\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\mathrm{sinx}\:\mathrm{dx}\:=\mathrm{f}\left(\mathrm{1}\right)=\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−\mathrm{e}^{−\mathrm{1}} \right) \\ $$$$=\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{e}}\right) \\ $$
Commented by mnjuly1970 last updated on 01/Jan/21
$$\:{thanks}\:{alot}\:{sir}\:{max}\:.. \\ $$
Commented by mathmax by abdo last updated on 01/Jan/21

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir} \\ $$
