Question Number 123454 by mnjuly1970 last updated on 25/Nov/20

$$\:\:\:\:\:\:\:\:\:\:\:\:…{nice}\:\:{calculus}… \\ $$$$\:\:\:\:\:{calculate}\:::: \\ $$$$\:\:\:\:\:\:\:\:\:\Omega\:\overset{???} {=}\int_{\mathrm{0}} ^{\:\infty} \sqrt{{x}}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left({cos}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)\right){dx} \\ $$
Answered by Olaf last updated on 25/Nov/20
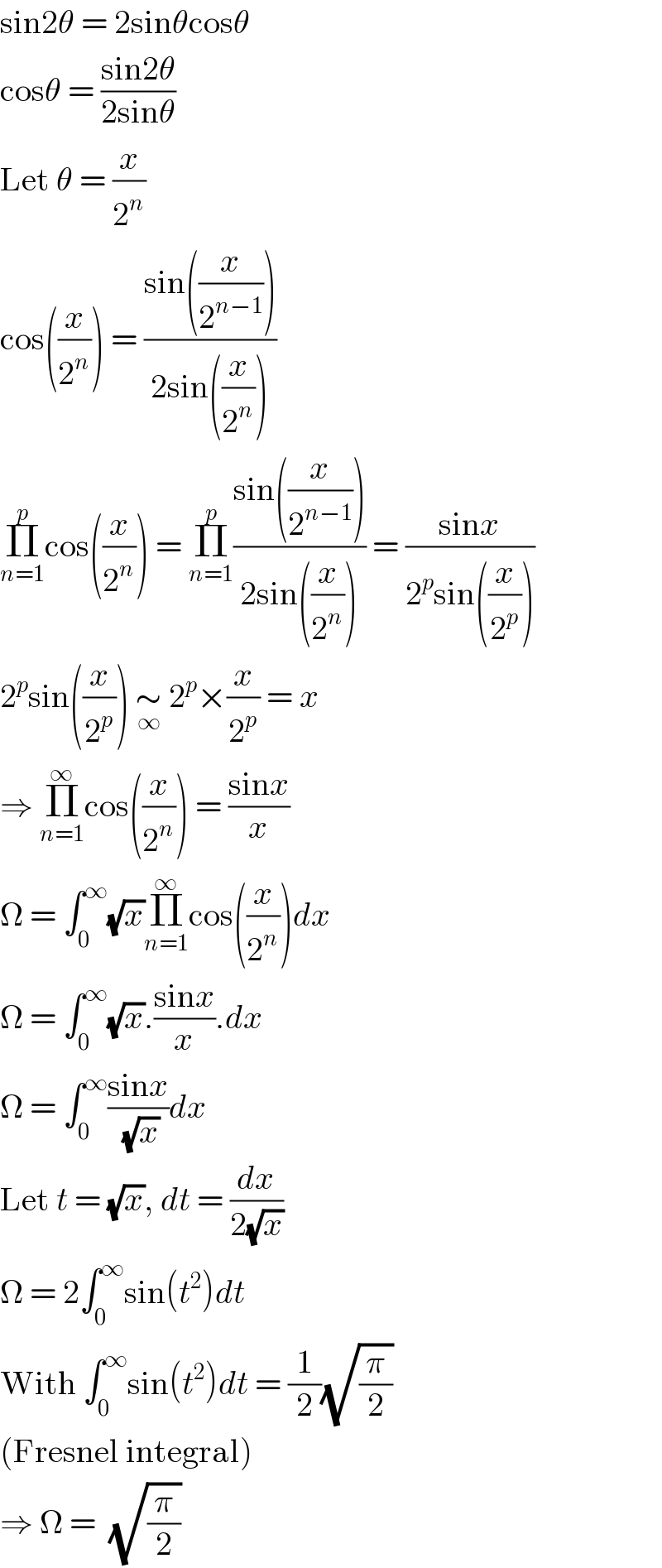
$$\mathrm{sin2}\theta\:=\:\mathrm{2sin}\theta\mathrm{cos}\theta \\ $$$$\mathrm{cos}\theta\:=\:\frac{\mathrm{sin2}\theta}{\mathrm{2sin}\theta} \\ $$$$\mathrm{Let}\:\theta\:=\:\frac{{x}}{\mathrm{2}^{{n}} } \\ $$$$\mathrm{cos}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)\:=\:\frac{\mathrm{sin}\left(\frac{{x}}{\mathrm{2}^{{n}−\mathrm{1}} }\right)}{\mathrm{2sin}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{p}} {\prod}}\mathrm{cos}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)\:=\:\underset{{n}=\mathrm{1}} {\overset{{p}} {\prod}}\frac{\mathrm{sin}\left(\frac{{x}}{\mathrm{2}^{{n}−\mathrm{1}} }\right)}{\mathrm{2sin}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)}\:=\:\frac{\mathrm{sin}{x}}{\mathrm{2}^{{p}} \mathrm{sin}\left(\frac{{x}}{\mathrm{2}^{{p}} }\right)} \\ $$$$\mathrm{2}^{{p}} \mathrm{sin}\left(\frac{{x}}{\mathrm{2}^{{p}} }\right)\:\underset{\infty} {\sim}\:\mathrm{2}^{{p}} ×\frac{{x}}{\mathrm{2}^{{p}} }\:=\:{x} \\ $$$$\Rightarrow\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\mathrm{cos}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)\:=\:\frac{\mathrm{sin}{x}}{{x}} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\infty} \sqrt{{x}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\mathrm{cos}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right){dx} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\infty} \sqrt{{x}}.\frac{\mathrm{sin}{x}}{{x}}.{dx} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{x}}{\:\sqrt{{x}}}{dx} \\ $$$$\mathrm{Let}\:{t}\:=\:\sqrt{{x}},\:{dt}\:=\:\frac{{dx}}{\mathrm{2}\sqrt{{x}}} \\ $$$$\Omega\:=\:\mathrm{2}\int_{\mathrm{0}} ^{\infty} \mathrm{sin}\left({t}^{\mathrm{2}} \right){dt} \\ $$$$\mathrm{With}\:\int_{\mathrm{0}} ^{\infty} \mathrm{sin}\left({t}^{\mathrm{2}} \right){dt}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\pi}{\mathrm{2}}} \\ $$$$\left(\mathrm{Fresnel}\:\mathrm{integral}\right) \\ $$$$\Rightarrow\:\Omega\:=\:\:\sqrt{\frac{\pi}{\mathrm{2}}} \\ $$
Commented by mnjuly1970 last updated on 26/Nov/20
$${thank}\:{you}\:{mr}\:{olaf}.{excellent} \\ $$
