Question Number 130432 by mnjuly1970 last updated on 25/Jan/21
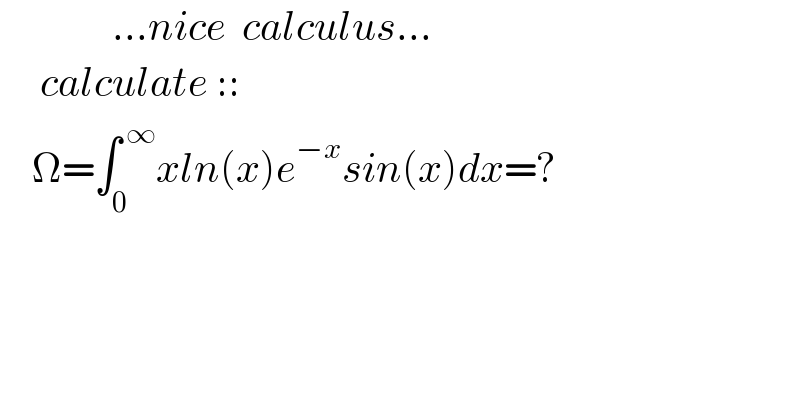
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:…{nice}\:\:{calculus}… \\ $$$$\:\:\:\:\:{calculate}\::: \\ $$$$\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\infty} {xln}\left({x}\right){e}^{−{x}} {sin}\left({x}\right){dx}=? \\ $$$$\:\:\: \\ $$
Answered by Dwaipayan Shikari last updated on 25/Jan/21
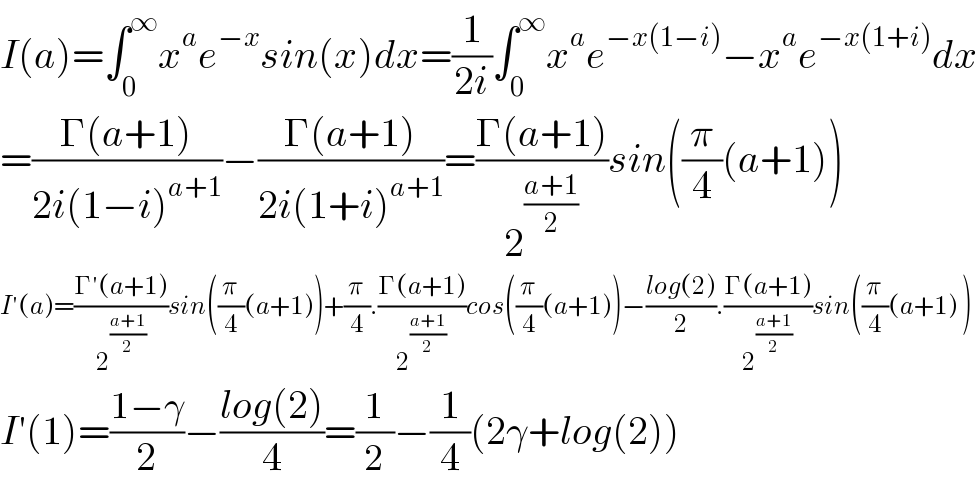
$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} {x}^{{a}} {e}^{−{x}} {sin}\left({x}\right){dx}=\frac{\mathrm{1}}{\mathrm{2}{i}}\int_{\mathrm{0}} ^{\infty} {x}^{{a}} {e}^{−{x}\left(\mathrm{1}−{i}\right)} −{x}^{{a}} {e}^{−{x}\left(\mathrm{1}+{i}\right)} {dx} \\ $$$$=\frac{\Gamma\left({a}+\mathrm{1}\right)}{\mathrm{2}{i}\left(\mathrm{1}−{i}\right)^{{a}+\mathrm{1}} }−\frac{\Gamma\left({a}+\mathrm{1}\right)}{\mathrm{2}{i}\left(\mathrm{1}+{i}\right)^{{a}+\mathrm{1}} }=\frac{\Gamma\left({a}+\mathrm{1}\right)}{\mathrm{2}^{\frac{{a}+\mathrm{1}}{\mathrm{2}}} }{sin}\left(\frac{\pi}{\mathrm{4}}\left({a}+\mathrm{1}\right)\right) \\ $$$${I}'\left({a}\right)=\frac{\Gamma'\left({a}+\mathrm{1}\right)}{\mathrm{2}^{\frac{{a}+\mathrm{1}}{\mathrm{2}}} }{sin}\left(\frac{\pi}{\mathrm{4}}\left({a}+\mathrm{1}\right)\right)+\frac{\pi}{\mathrm{4}}.\frac{\Gamma\left({a}+\mathrm{1}\right)}{\mathrm{2}^{\frac{{a}+\mathrm{1}}{\mathrm{2}}} }{cos}\left(\frac{\pi}{\mathrm{4}}\left({a}+\mathrm{1}\right)\right)−\frac{{log}\left(\mathrm{2}\right)}{\mathrm{2}}.\frac{\Gamma\left({a}+\mathrm{1}\right)}{\mathrm{2}^{\frac{{a}+\mathrm{1}}{\mathrm{2}}} }{sin}\left(\frac{\pi}{\mathrm{4}}\left({a}+\mathrm{1}\right)\:\right) \\ $$$${I}'\left(\mathrm{1}\right)=\frac{\mathrm{1}−\gamma}{\mathrm{2}}−\frac{{log}\left(\mathrm{2}\right)}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{2}\gamma+{log}\left(\mathrm{2}\right)\right) \\ $$
