Question Number 127958 by mnjuly1970 last updated on 03/Jan/21
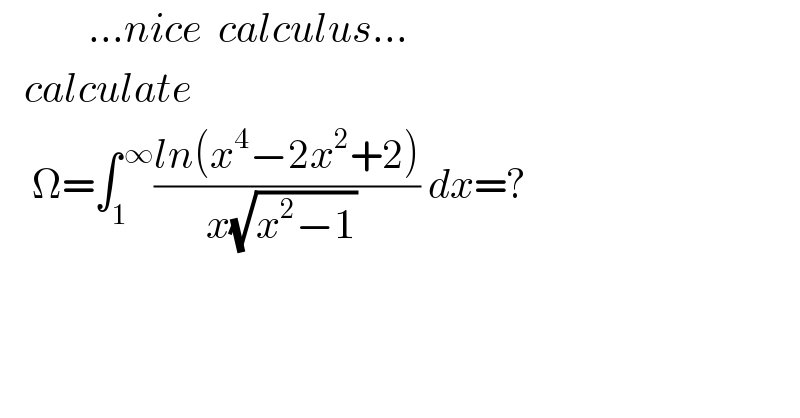
$$\:\:\:\:\:\:\:\:\:\:\:…{nice}\:\:{calculus}… \\ $$$$\:\:\:{calculate} \\ $$$$\:\:\:\:\Omega=\int_{\mathrm{1}} ^{\:\infty} \frac{{ln}\left({x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}\right)}{{x}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:}\:{dx}=? \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 03/Jan/21
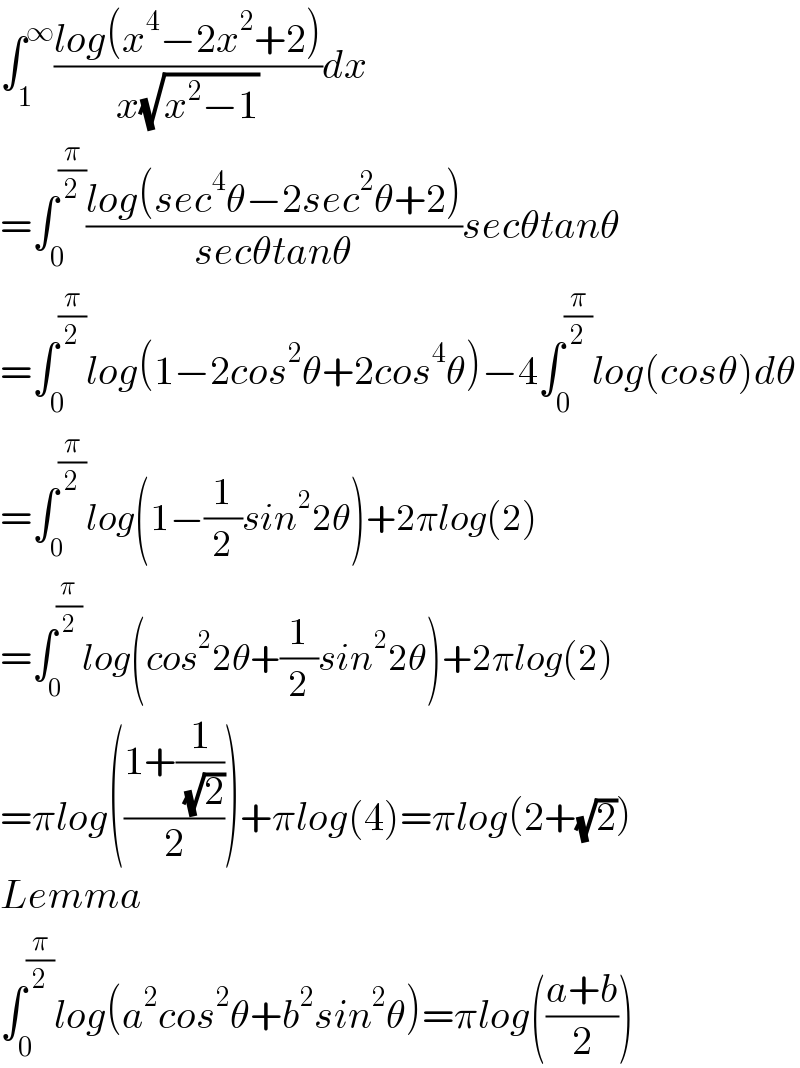
$$\int_{\mathrm{1}} ^{\infty} \frac{{log}\left({x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}\right)}{{x}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{log}\left({sec}^{\mathrm{4}} \theta−\mathrm{2}{sec}^{\mathrm{2}} \theta+\mathrm{2}\right)}{{sec}\theta{tan}\theta}{sec}\theta{tan}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left(\mathrm{1}−\mathrm{2}{cos}^{\mathrm{2}} \theta+\mathrm{2}{cos}^{\mathrm{4}} \theta\right)−\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({cos}\theta\right){d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{sin}^{\mathrm{2}} \mathrm{2}\theta\right)+\mathrm{2}\pi{log}\left(\mathrm{2}\right) \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({cos}^{\mathrm{2}} \mathrm{2}\theta+\frac{\mathrm{1}}{\mathrm{2}}{sin}^{\mathrm{2}} \mathrm{2}\theta\right)+\mathrm{2}\pi{log}\left(\mathrm{2}\right) \\ $$$$=\pi{log}\left(\frac{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}{\mathrm{2}}\right)+\pi{log}\left(\mathrm{4}\right)=\pi{log}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right) \\ $$$${Lemma} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({a}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta\right)=\pi{log}\left(\frac{{a}+{b}}{\mathrm{2}}\right) \\ $$
