Question Number 130949 by mnjuly1970 last updated on 31/Jan/21
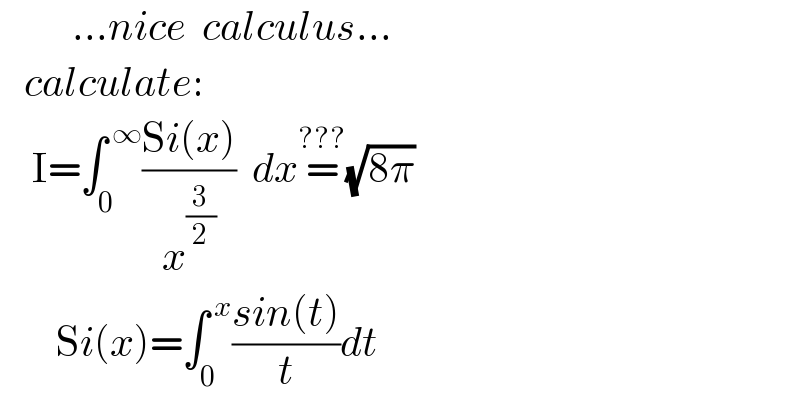
$$\:\:\:\:\:\:\:\:\:…{nice}\:\:{calculus}… \\ $$$$\:\:\:{calculate}:\: \\ $$$$\:\:\:\:\mathrm{I}=\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{S}{i}\left({x}\right)}{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }\:\:{dx}\overset{???} {=}\sqrt{\mathrm{8}\pi}\: \\ $$$$\:\:\:\:\:\:\:\mathrm{S}{i}\left({x}\right)=\int_{\mathrm{0}} ^{\:{x}} \frac{{sin}\left({t}\right)}{{t}}{dt} \\ $$
Answered by mindispower last updated on 31/Jan/21

$$\int\frac{{si}\left({x}\right)}{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }{dx}=−\frac{\mathrm{2}{si}\left({x}\right)}{\:\sqrt{{x}}}+\mathrm{2}\int\frac{{sin}\left({x}\right)}{\:\sqrt{{x}}.{x}}{dx} \\ $$$${put}\:{x}={u}^{\mathrm{2}} ,{in}\:\mathrm{2}{nd} \\ $$$$\mathrm{2}\int\frac{{sin}\left({x}\right)}{{x}\sqrt{{x}}}{dx}=\mathrm{4}\int\frac{{sin}\left({u}^{\mathrm{2}} \right)}{{u}^{\mathrm{2}} }{du} \\ $$$${by}\:{part}=−\frac{\mathrm{4}{sin}\left({u}^{\mathrm{2}} \right)}{{u}}+\mathrm{8}\int{cos}\left({u}^{\mathrm{2}} \right){du}…{E} \\ $$$$\int_{\mathrm{0}} ^{{t}} {cos}\left(\frac{\pi}{\mathrm{2}}{x}^{\mathrm{2}} \right){dx}={C}\left({t}\right)\:{fersnel}\:{integral} \\ $$$${u}=\sqrt{\frac{\pi}{\mathrm{2}}\:}{y} \\ $$$$\int\sqrt{\frac{\pi}{\mathrm{2}}}{ycos}\left(\frac{\pi{y}^{\mathrm{2}} }{\mathrm{2}}\right){dy}=\sqrt{\frac{\pi}{\mathrm{2}}}{C}\left({y}\right) \\ $$$${we}\:{get} \\ $$$${E}=−\frac{\mathrm{4}{sin}\left({u}^{\mathrm{2}} \right)}{{u}}+\mathrm{4}\sqrt{\mathrm{2}\pi}{C}\left(\sqrt{\frac{\mathrm{2}}{\pi}}{u}\right) \\ $$$$\int\frac{{si}\left({x}\right)}{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }{dx}=\frac{−\mathrm{2}{si}\left({x}\right)}{\:\sqrt{{x}}}−\frac{\mathrm{4}{sin}\left({x}\right)}{\:\sqrt{{x}}}+\mathrm{4}\sqrt{\mathrm{2}\pi}.{C}\left(\sqrt{\frac{\mathrm{2}}{\pi}}.\sqrt{{x}}\right) \\ $$$${x}\rightarrow\infty \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}{C}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \frac{{si}\left({x}\right)}{{x}\sqrt{{x}}}{dx}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(−\frac{\mathrm{2}{si}\left({x}\right)}{\:\sqrt{{x}}}−\frac{\mathrm{4}{sin}\left({x}\right)}{\:\sqrt{{x}}}+\mathrm{4}\sqrt{\mathrm{2}\pi}{Ci}\left(\sqrt{\frac{\mathrm{2}{x}}{\pi}}\right)\right) \\ $$$$=\mathrm{2}\sqrt{\mathrm{2}\pi}=\sqrt{\mathrm{8}\pi} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 31/Jan/21
$${very}\:{nice}\:{as}\:{always} \\ $$$${sir}\:\:{mindispower}… \\ $$$$\:{Allah}\:{keep}\:{you}.. \\ $$
Commented by mindispower last updated on 31/Jan/21
$${inshallah}\:{alaways}\:{withe}\:{pleasur} \\ $$
