Question Number 129988 by mnjuly1970 last updated on 21/Jan/21
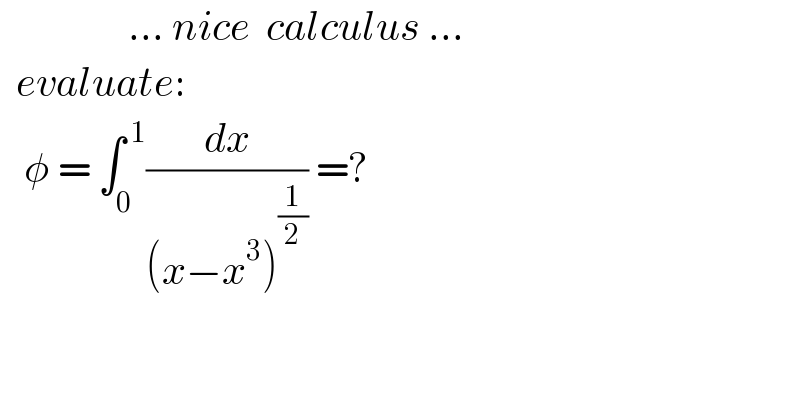
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\:{nice}\:\:{calculus}\:… \\ $$$$\:\:{evaluate}:\: \\ $$$$\:\:\:\phi\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{dx}}{\left({x}−{x}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} }\:=? \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 21/Jan/21
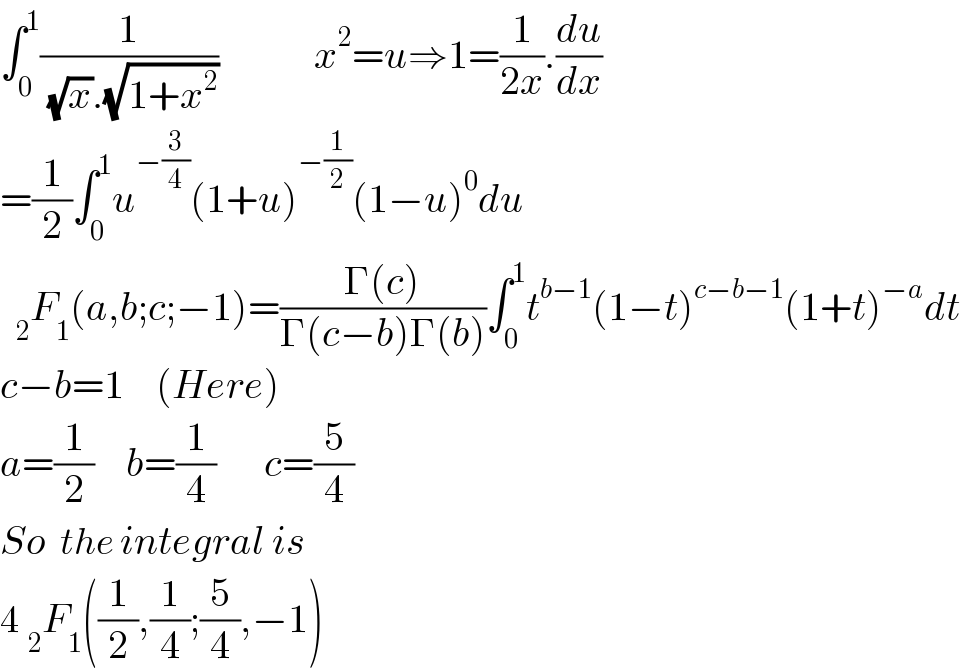
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{{x}}.\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} ={u}\Rightarrow\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}{x}}.\frac{{du}}{{dx}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{−\frac{\mathrm{3}}{\mathrm{4}}} \left(\mathrm{1}+{u}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−{u}\right)^{\mathrm{0}} {du} \\ $$$$\:\:_{\mathrm{2}} {F}_{\mathrm{1}} \left({a},{b};{c};−\mathrm{1}\right)=\frac{\Gamma\left({c}\right)}{\Gamma\left({c}−{b}\right)\Gamma\left({b}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{b}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{c}−{b}−\mathrm{1}} \left(\mathrm{1}+{t}\right)^{−{a}} {dt} \\ $$$${c}−{b}=\mathrm{1}\:\:\:\:\left({Here}\right) \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:{b}=\frac{\mathrm{1}}{\mathrm{4}}\:\:\:\:\:\:{c}=\frac{\mathrm{5}}{\mathrm{4}} \\ $$$${So}\:\:{the}\:{integral}\:{is}\: \\ $$$$\mathrm{4}\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{4}};\frac{\mathrm{5}}{\mathrm{4}},−\mathrm{1}\right) \\ $$
Answered by Dwaipayan Shikari last updated on 21/Jan/21
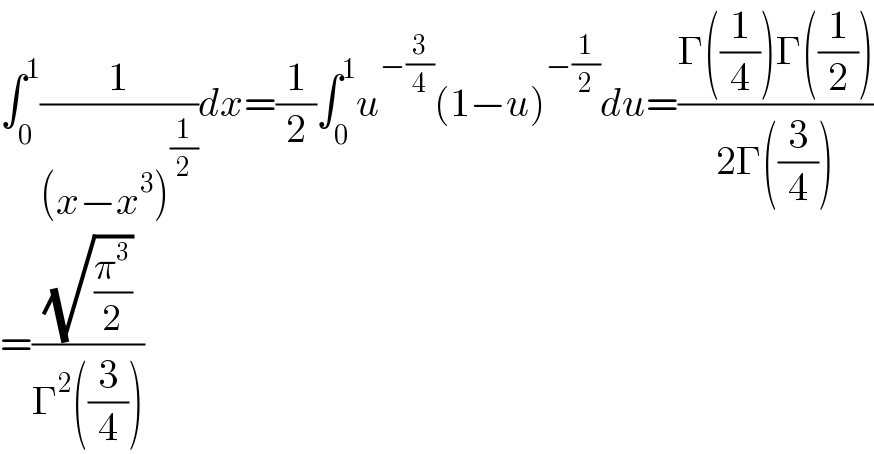
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left({x}−{x}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{−\frac{\mathrm{3}}{\mathrm{4}}} \left(\mathrm{1}−{u}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {du}=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)} \\ $$$$=\frac{\sqrt{\frac{\pi^{\mathrm{3}} }{\mathrm{2}}}}{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)} \\ $$
Commented by mnjuly1970 last updated on 22/Jan/21

$${thanks}\:{alot}… \\ $$
Answered by mathmax by abdo last updated on 21/Jan/21
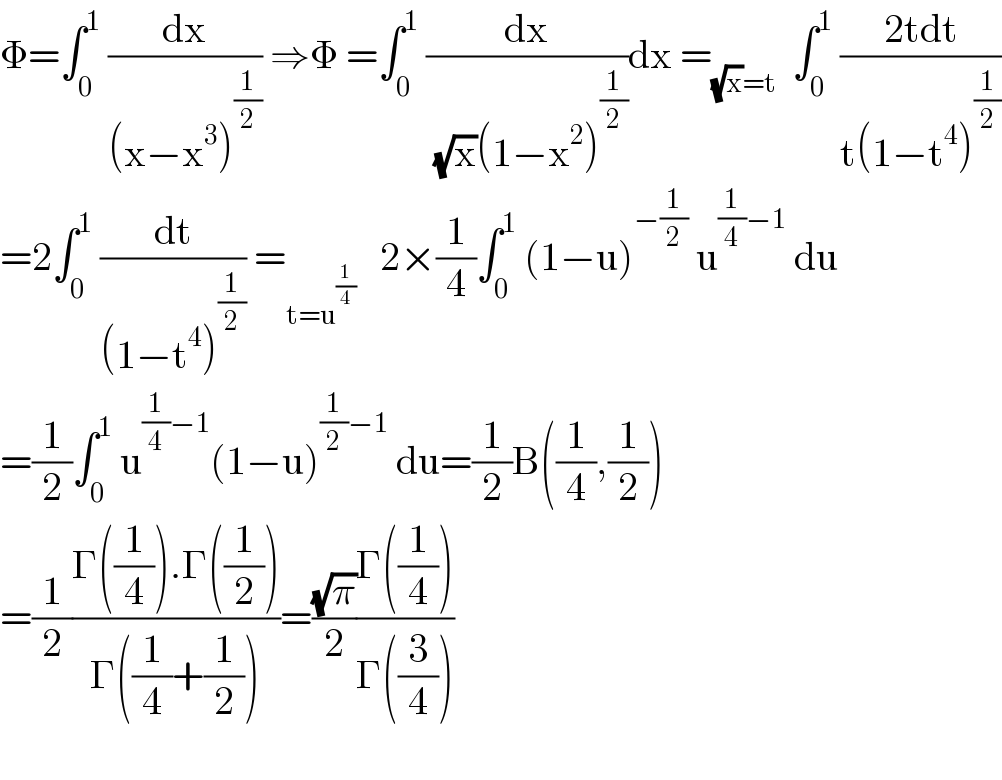
$$\Phi=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\left(\mathrm{x}−\mathrm{x}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} }\:\Rightarrow\Phi\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} }\mathrm{dx}\:=_{\sqrt{\mathrm{x}}=\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2tdt}}{\mathrm{t}\left(\mathrm{1}−\mathrm{t}^{\mathrm{4}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} } \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\left(\mathrm{1}−\mathrm{t}^{\mathrm{4}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} }\:=_{\mathrm{t}=\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{4}}} } \:\:\:\mathrm{2}×\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\mathrm{1}−\mathrm{u}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} \:\mathrm{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} \left(\mathrm{1}−\mathrm{u}\right)^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \:\mathrm{du}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{B}\left(\frac{\mathrm{1}}{\mathrm{4}},\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right).\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\right)}=\frac{\sqrt{\pi}}{\mathrm{2}}\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 22/Jan/21
$${grateful}\:{sir}\:{max}\:… \\ $$
