Menu Close

nice-calculus-evaluate-0-ln-x-x-2-1-3-dx-

Tinku Tara 0 Comments
Pin




Question Number 127539 by mnjuly1970 last updated on 30/Dec/20
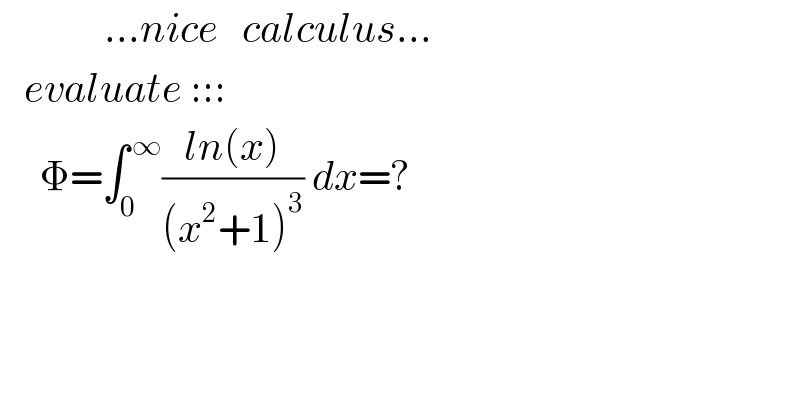
...nice calculus... evaluate ::: Φ=∫_0 ^( ∞) ((ln(x))/((x^2 +1)^3 )) dx=?
$$\:\:\:\:\:\:\:\:\:\:\:\:\:…{nice}\:\:\:{calculus}… \\ $$$$\:\:\:{evaluate}\:::: \\ $$$$\:\:\:\:\:\Phi=\int_{\mathrm{0}} ^{\:\infty} \frac{{ln}\left({x}\right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\:{dx}=? \\ $$$$ \\ $$
Answered by Lordose last updated on 30/Dec/20
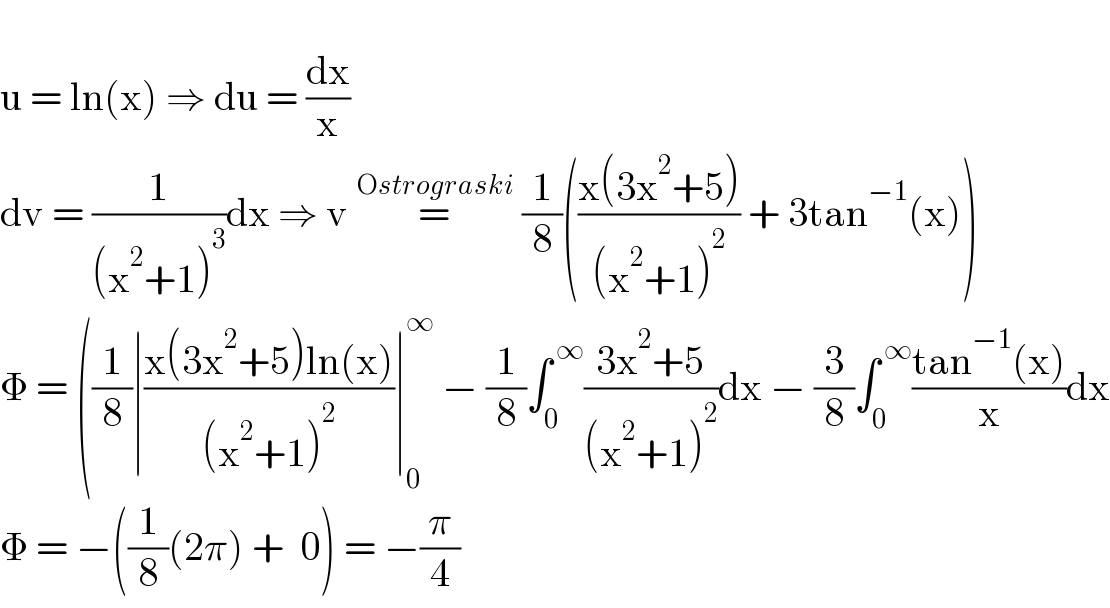
u = ln(x) ⇒ du = (dx/x) dv = (1/((x^2 +1)^3 ))dx ⇒ v =^(Ostrograski) (1/8)(((x(3x^2 +5))/((x^2 +1)^2 )) + 3tan^(−1) (x)) Φ = ((1/8)∣((x(3x^2 +5)ln(x))/((x^2 +1)^2 ))∣_0 ^∞ − (1/8)∫_0 ^( ∞) ((3x^2 +5)/((x^2 +1)^2 ))dx − (3/8)∫_0 ^( ∞) ((tan^(−1) (x))/x)dx Φ = −((1/8)(2π) + 0) = −(π/4)
$$ \\ $$$$\mathrm{u}\:=\:\mathrm{ln}\left(\mathrm{x}\right)\:\Rightarrow\:\mathrm{du}\:=\:\frac{\mathrm{dx}}{\mathrm{x}} \\ $$$$\mathrm{dv}\:=\:\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dx}\:\Rightarrow\:\mathrm{v}\:\overset{\mathrm{O}{strograski}} {=}\:\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{x}\left(\mathrm{3x}^{\mathrm{2}} +\mathrm{5}\right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:+\:\mathrm{3tan}^{−\mathrm{1}} \left(\mathrm{x}\right)\right) \\ $$$$\Phi\:=\:\left(\frac{\mathrm{1}}{\mathrm{8}}\mid\frac{\mathrm{x}\left(\mathrm{3x}^{\mathrm{2}} +\mathrm{5}\right)\mathrm{ln}\left(\mathrm{x}\right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mid_{\mathrm{0}} ^{\infty} \:−\:\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{3x}^{\mathrm{2}} +\mathrm{5}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:−\:\frac{\mathrm{3}}{\mathrm{8}}\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}\right. \\ $$$$\Phi\:=\:−\left(\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{2}\pi\right)\:+\:\:\mathrm{0}\right)\:=\:−\frac{\pi}{\mathrm{4}} \\ $$
Answered by mathmax by abdo last updated on 01/Jan/21
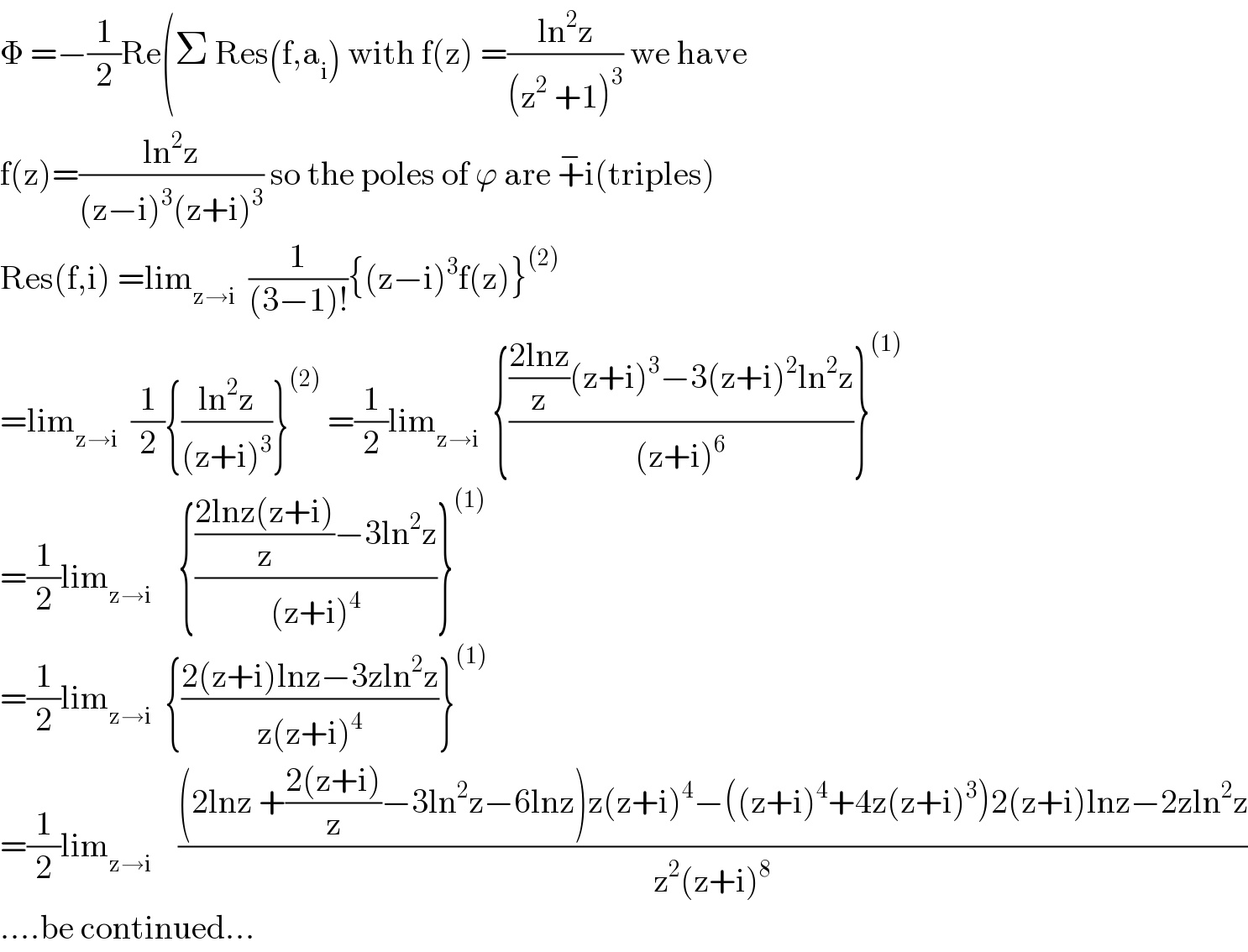
Φ =−(1/2)Re(Σ Res(f,a_i ) with f(z) =((ln^2 z)/((z^2 +1)^3 )) we have f(z)=((ln^2 z)/((z−i)^3 (z+i)^3 )) so the poles of ϕ are +^− i(triples) Res(f,i) =lim_(z→i) (1/((3−1)!)){(z−i)^3 f(z)}^((2)) =lim_(z→i) (1/2){((ln^2 z)/((z+i)^3 ))}^((2)) =(1/2)lim_(z→i) {((((2lnz)/z)(z+i)^3 −3(z+i)^2 ln^2 z)/((z+i)^6 ))}^((1)) =(1/2)lim_(z→i) {((((2lnz(z+i))/z)−3ln^2 z)/((z+i)^4 ))}^((1)) =(1/2)lim_(z→i) {((2(z+i)lnz−3zln^2 z)/(z(z+i)^4 ))}^((1)) =(1/2)lim_(z→i) (((2lnz +((2(z+i))/z)−3ln^2 z−6lnz)z(z+i)^4 −((z+i)^4 +4z(z+i)^3 )2(z+i)lnz−2zln^2 z)/(z^2 (z+i)^8 )) ....be continued...
$$\Phi\:=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Re}\left(\Sigma\:\mathrm{Res}\left(\mathrm{f},\mathrm{a}_{\mathrm{i}} \right)\:\mathrm{with}\:\mathrm{f}\left(\mathrm{z}\right)\:=\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} }\:\mathrm{we}\:\mathrm{have}\:\right. \\ $$$$\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{3}} \left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{3}} }\:\mathrm{so}\:\mathrm{the}\:\mathrm{poles}\:\mathrm{of}\:\varphi\:\mathrm{are}\:\overset{−} {+}\mathrm{i}\left(\mathrm{triples}\right) \\ $$$$\mathrm{Res}\left(\mathrm{f},\mathrm{i}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\frac{\mathrm{1}}{\left(\mathrm{3}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{3}} \mathrm{f}\left(\mathrm{z}\right)\right\}^{\left(\mathrm{2}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{3}} }\right\}^{\left(\mathrm{2}\right)} \:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\left\{\frac{\frac{\mathrm{2lnz}}{\mathrm{z}}\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{3}} −\mathrm{3}\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} \mathrm{ln}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{6}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\:\left\{\frac{\frac{\mathrm{2lnz}\left(\mathrm{z}+\mathrm{i}\right)}{\mathrm{z}}−\mathrm{3ln}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{4}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\left\{\frac{\mathrm{2}\left(\mathrm{z}+\mathrm{i}\right)\mathrm{lnz}−\mathrm{3zln}^{\mathrm{2}} \mathrm{z}}{\mathrm{z}\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{4}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\:\frac{\left(\mathrm{2lnz}\:+\frac{\mathrm{2}\left(\mathrm{z}+\mathrm{i}\right)}{\mathrm{z}}−\mathrm{3ln}^{\mathrm{2}} \mathrm{z}−\mathrm{6lnz}\right)\mathrm{z}\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{4}} −\left(\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{4}} +\mathrm{4z}\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{3}} \right)\mathrm{2}\left(\mathrm{z}+\mathrm{i}\right)\mathrm{lnz}−\mathrm{2zln}^{\mathrm{2}} \mathrm{z}}{\mathrm{z}^{\mathrm{2}} \left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{8}} } \\ $$$$….\mathrm{be}\:\mathrm{continued}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *