Question Number 124887 by mnjuly1970 last updated on 06/Dec/20
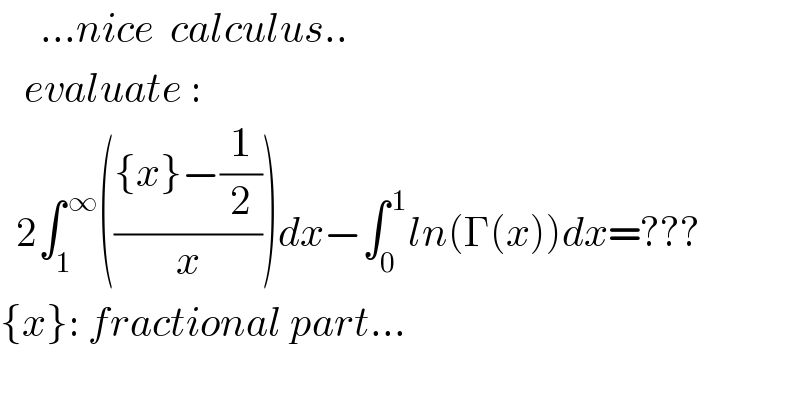
$$\:\:\:\:\:…{nice}\:\:{calculus}.. \\ $$$$\:\:\:{evaluate}\:: \\ $$$$\:\:\mathrm{2}\int_{\mathrm{1}} ^{\:\infty} \left(\frac{\left\{{x}\right\}−\frac{\mathrm{1}}{\mathrm{2}}}{{x}}\right){dx}−\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\left(\Gamma\left({x}\right)\right){dx}=??? \\ $$$$\left\{{x}\right\}:\:{fractional}\:{part}… \\ $$
Answered by Dwaipayan Shikari last updated on 06/Dec/20
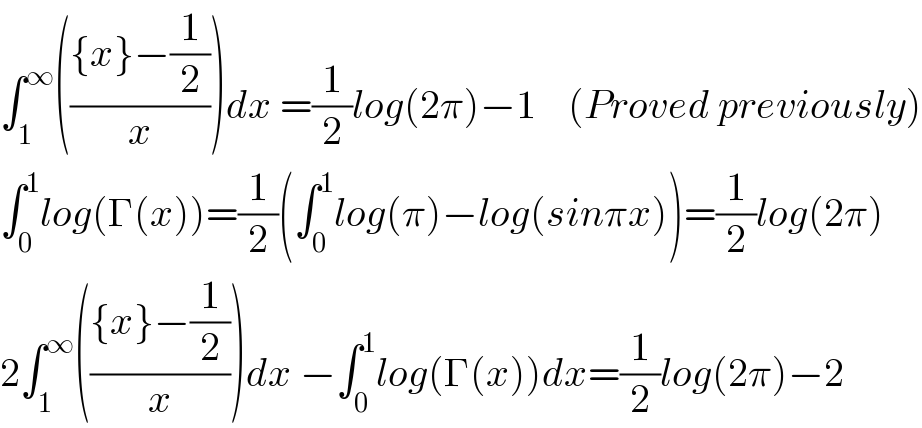
$$\int_{\mathrm{1}} ^{\infty} \left(\frac{\left\{{x}\right\}−\frac{\mathrm{1}}{\mathrm{2}}}{{x}}\right){dx}\:=\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{2}\pi\right)−\mathrm{1}\:\:\:\:\left({Proved}\:{previously}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {log}\left(\Gamma\left({x}\right)\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\int_{\mathrm{0}} ^{\mathrm{1}} {log}\left(\pi\right)−{log}\left({sin}\pi{x}\right)\right)=\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{2}\pi\right) \\ $$$$\mathrm{2}\int_{\mathrm{1}} ^{\infty} \left(\frac{\left\{{x}\right\}−\frac{\mathrm{1}}{\mathrm{2}}}{{x}}\right){dx}\:−\int_{\mathrm{0}} ^{\mathrm{1}} {log}\left(\Gamma\left({x}\right)\right){dx}=\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{2}\pi\right)−\mathrm{2}\:\: \\ $$
Commented by mnjuly1970 last updated on 06/Dec/20

$${excellent}… \\ $$
