Menu Close

nice-calculus-evaluate-k-0-m-0-n-0-1-k-m-n-

Tinku Tara 0 Comments
Pin




Question Number 129926 by mnjuly1970 last updated on 20/Jan/21
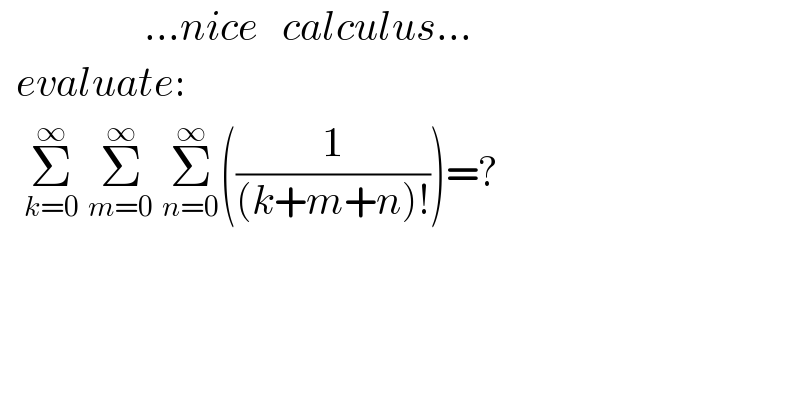
...nice calculus... evaluate: Σ_(k=0) ^∞ Σ_(m=0) ^∞ Σ_(n=0) ^∞ ((1/((k+m+n)!)))=?
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…{nice}\:\:\:{calculus}… \\ $$$$\:\:{evaluate}: \\ $$$$\:\:\:\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\:\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\left({k}+{m}+{n}\right)!}\right)=? \\ $$$$ \\ $$
Answered by mindispower last updated on 22/Jan/21
Σ_(a,b≥1) (1/((a+b)!))=((Γ(a+1)Γ(b))/(Γ(a+1+b)a!.(b−1)!)) =Σ_(a≥1) (1/(a!)).Σ_(b≥1) .((β(a+1,b))/((b−1)!)) β(a+1,b)=∫_0 ^1 t^(b−1) (1−t)^a .dt Σ(1/(a!)).∫_0 ^1 Σ_(b≥1) (t^(b−1) /((b−1)!))(1−t)^a dt =∫_0 ^1 e^t .Σ_(a≥1) (((1−t)^a )/(a!))dt =∫_0 ^1 e^t (e^((1−t)) −1)dt. =∫_0 ^1 e−e^t dt=e−(e−1)=1 ΣΣΣ(1/((a+b+c)!))=Σ_a Σ_b .(1/((a+b)!))+Σ_a .Σ_b Σ_(c≥1) ((Γ(a+b+1)Γ(c))/(Γ(a+b+1+c)(c−1)!.(a+b)!)) first done Σ_(a≥0) Σ_(b≥0) (1/((a+b)!))Σ_(c≥1) .((β(a+b+1,c))/((c−1)!)) =Σ_a Σ_b (1/((a+b)!))Σ_(c≥1) ∫_0 ^1 (1−t)^(a+b) t^(c−1) (dt/((c−1)!)) =Σ_a Σ_b (1/((a+b)!))∫_0 ^1 (1−t)^(a+b) e^t dt =Σ_(a≥0) Σ_(b≥1) .((Γ(a+1)Γ(b))/(a!(b−1)!Γ(a+1+b)))∫_0 ^1 (1−t)^(a+b) e^t dt +Σ_(a≥0) (1/(a!))∫_0 ^1 (1−t)^a e^t dt_(=e) =Σ_(a≥0) (1/(a!))Σ_(b≥1) (1/((b−1)))∫_0 ^1 s^a (1−s)^(b−1) ds∫_0 ^1 (1−t)^(a+b) e^t dt +e =e+Σ_(a≥0) (1/(a!))∫_0 ^1 ∫_0 ^1 Σ_(b≥1) (1/((b−1)!))(s(1−t))^a .((1−s)(1−t))^(b−1) (1−t).dtds =e+∫_0 ^1 ∫_0 ^1 Σ_(a≥0) (((s(1−t))^a )/(a!)).Σ_(b≥1) ((((1−s)(1−t))^(b−1) )/(b−1)).(1−t)dt =e+∫_0 ^1 .∫_0 ^1 .e^(s(1−t)) .e^((1−s)(1−t)) (1−t)e^t dt =e+∫_0 ^1 (1−t)edt=(3/2)e
$$\underset{{a},{b}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left({a}+{b}\right)!}=\frac{\Gamma\left({a}+\mathrm{1}\right)\Gamma\left({b}\right)}{\Gamma\left({a}+\mathrm{1}+{b}\right){a}!.\left({b}−\mathrm{1}\right)!} \\ $$$$=\underset{{a}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{a}!}.\underset{{b}\geqslant\mathrm{1}} {\sum}.\frac{\beta\left({a}+\mathrm{1},{b}\right)}{\left({b}−\mathrm{1}\right)!} \\ $$$$\beta\left({a}+\mathrm{1},{b}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{b}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{a}} .{dt} \\ $$$$\Sigma\frac{\mathrm{1}}{{a}!}.\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{b}\geqslant\mathrm{1}} {\sum}\frac{{t}^{{b}−\mathrm{1}} }{\left({b}−\mathrm{1}\right)!}\left(\mathrm{1}−{t}\right)^{{a}} {dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{t}} .\underset{{a}\geqslant\mathrm{1}} {\sum}\frac{\left(\mathrm{1}−{t}\right)^{{a}} }{{a}!}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{t}} \left({e}^{\left(\mathrm{1}−{t}\right)} −\mathrm{1}\right){dt}. \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {e}−{e}^{{t}} {dt}={e}−\left({e}−\mathrm{1}\right)=\mathrm{1} \\ $$$$\Sigma\Sigma\Sigma\frac{\mathrm{1}}{\left({a}+{b}+{c}\right)!}=\underset{{a}} {\sum}\underset{{b}} {\sum}.\frac{\mathrm{1}}{\left({a}+{b}\right)!}+\underset{{a}} {\sum}.\underset{{b}} {\sum}\underset{{c}\geqslant\mathrm{1}} {\sum}\frac{\Gamma\left({a}+{b}+\mathrm{1}\right)\Gamma\left({c}\right)}{\Gamma\left({a}+{b}+\mathrm{1}+{c}\right)\left({c}−\mathrm{1}\right)!.\left({a}+{b}\right)!} \\ $$$${first}\:{done} \\ $$$$\underset{{a}\geqslant\mathrm{0}} {\sum}\underset{{b}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left({a}+{b}\right)!}\underset{{c}\geqslant\mathrm{1}} {\sum}.\frac{\beta\left({a}+{b}+\mathrm{1},{c}\right)}{\left({c}−\mathrm{1}\right)!} \\ $$$$=\underset{{a}} {\sum}\underset{{b}} {\sum}\frac{\mathrm{1}}{\left({a}+{b}\right)!}\underset{{c}\geqslant\mathrm{1}} {\sum}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{a}+{b}} {t}^{{c}−\mathrm{1}} \frac{{dt}}{\left({c}−\mathrm{1}\right)!} \\ $$$$=\underset{{a}} {\sum}\underset{{b}} {\sum}\frac{\mathrm{1}}{\left({a}+{b}\right)!}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{a}+{b}} {e}^{{t}} {dt} \\ $$$$=\underset{{a}\geqslant\mathrm{0}} {\sum}\underset{{b}\geqslant\mathrm{1}} {\sum}.\frac{\Gamma\left({a}+\mathrm{1}\right)\Gamma\left({b}\right)}{{a}!\left({b}−\mathrm{1}\right)!\Gamma\left({a}+\mathrm{1}+{b}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{a}+{b}} {e}^{{t}} {dt} \\ $$$$+\underset{{a}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{{a}!}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{a}} {e}^{{t}} {d}\underset{={e}} {{t}} \\ $$$$=\underset{{a}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{{a}!}\underset{{b}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left({b}−\mathrm{1}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} {s}^{{a}} \left(\mathrm{1}−{s}\right)^{{b}−\mathrm{1}} {ds}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{a}+{b}} {e}^{{t}} {dt} \\ $$$$+{e} \\ $$$$={e}+\underset{{a}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{{a}!}\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \underset{{b}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left({b}−\mathrm{1}\right)!}\left({s}\left(\mathrm{1}−{t}\right)\right)^{{a}} .\left(\left(\mathrm{1}−{s}\right)\left(\mathrm{1}−{t}\right)\right)^{{b}−\mathrm{1}} \left(\mathrm{1}−{t}\right).{dtds} \\ $$$$={e}+\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \underset{{a}\geqslant\mathrm{0}} {\sum}\frac{\left({s}\left(\mathrm{1}−{t}\right)\right)^{{a}} }{{a}!}.\underset{{b}\geqslant\mathrm{1}} {\sum}\frac{\left(\left(\mathrm{1}−{s}\right)\left(\mathrm{1}−{t}\right)\right)^{{b}−\mathrm{1}} }{{b}−\mathrm{1}}.\left(\mathrm{1}−{t}\right){dt} \\ $$$$={e}+\int_{\mathrm{0}} ^{\mathrm{1}} .\int_{\mathrm{0}} ^{\mathrm{1}} .{e}^{{s}\left(\mathrm{1}−{t}\right)} .{e}^{\left(\mathrm{1}−{s}\right)\left(\mathrm{1}−{t}\right)} \left(\mathrm{1}−{t}\right){e}^{{t}} {dt} \\ $$$$={e}+\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{t}\right){edt}=\frac{\mathrm{3}}{\mathrm{2}}{e} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *