Question Number 123060 by mnjuly1970 last updated on 22/Nov/20
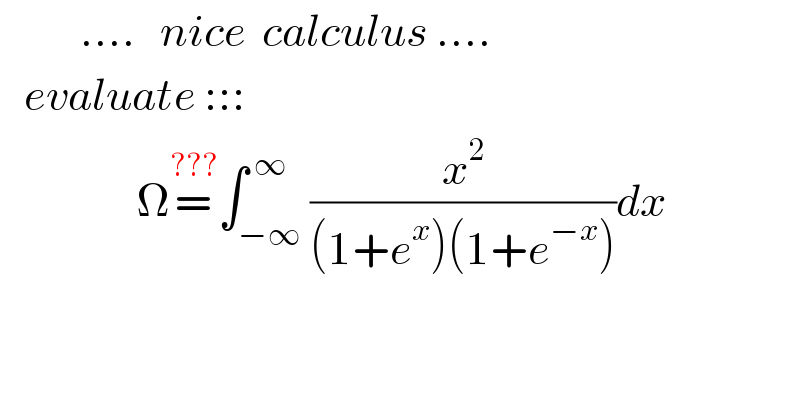
$$\:\:\:\:\:\:\:\:\:\:….\:\:\:{nice}\:\:{calculus}\:…. \\ $$$$\:\:\:{evaluate}\:::: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Omega\overset{???} {=}\int_{−\infty} ^{\:\infty} \frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+{e}^{{x}} \right)\left(\mathrm{1}+{e}^{−{x}} \right)}{dx} \\ $$
Answered by mindispower last updated on 22/Nov/20
![=2∫_0 ^∞ ((e^x x^2 )/((1+e^x )^2 )) =2[−(x^2 /(1+e^x ))]_0 ^∞ +4∫_0 ^∞ (x/(1+e^x ))dx =4∫_0 ^∞ xΣ(−1e^(−x) )^k e^(−x) dx =4Σ_(k≥0) ∫_0 ^∞ (−1)^k e^(−(1+k)x) xdx =4Σ_(k≥0) ∫_0 ^∞ (((−1)^k )/((1+k)^2 ))xe^(−x) dx =4Σ(((−1)^k )/((1+k)^2 ))=4(((ζ(2))/2))=(π^2 /3)](https://www.tinkutara.com/question/Q123069.png)
$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{{e}^{{x}} {x}^{\mathrm{2}} }{\left(\mathrm{1}+{e}^{{x}} \right)^{\mathrm{2}} } \\ $$$$=\mathrm{2}\left[−\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{e}^{{x}} }\right]_{\mathrm{0}} ^{\infty} +\mathrm{4}\int_{\mathrm{0}} ^{\infty} \frac{{x}}{\mathrm{1}+{e}^{{x}} }{dx} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\infty} {x}\Sigma\left(−\mathrm{1}{e}^{−{x}} \right)^{{k}} {e}^{−{x}} {dx} \\ $$$$=\mathrm{4}\underset{{k}\geqslant\mathrm{0}} {\sum}\int_{\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{k}} {e}^{−\left(\mathrm{1}+{k}\right){x}} {xdx} \\ $$$$=\mathrm{4}\underset{{k}\geqslant\mathrm{0}} {\sum}\int_{\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{k}} }{\left(\mathrm{1}+{k}\right)^{\mathrm{2}} }{xe}^{−{x}} {dx} \\ $$$$=\mathrm{4}\Sigma\frac{\left(−\mathrm{1}\right)^{{k}} }{\left(\mathrm{1}+{k}\right)^{\mathrm{2}} }=\mathrm{4}\left(\frac{\zeta\left(\mathrm{2}\right)}{\mathrm{2}}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{3}} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 22/Nov/20
$${grateful} \\ $$$${mr}\:{mindspower}… \\ $$
Answered by Dwaipayan Shikari last updated on 22/Nov/20
![2∫_0 ^∞ ((x^2 e^x )/((1+e^x )^2 ))dx =4x∫_0 ^∞ (e^x /((1+e^x )^2 ))dx−∫_0 ^∞ 4x∫(e^x /((1+e^x )^2 )) =−[((2x)/((1+e^x )))]_0 ^∞ +4∫_0 ^∞ (x/((1+e^x )))dx =4Σ_(n=1) ^∞ (−1)^(n+1) ∫_0 ^∞ xe^(−nx) dx =4Σ_(n=1) ^∞ (−1)^(n+1) (1/n^2 )∫_0 ^∞ ue^(−u) du =4Σ^∞ (((−1)^(n+1) )/n^2 )Γ(2)=(π^2 /(12)).4=(π^2 /3)](https://www.tinkutara.com/question/Q123074.png)
$$\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}} {e}^{{x}} }{\left(\mathrm{1}+{e}^{{x}} \right)^{\mathrm{2}} }{dx} \\ $$$$=\mathrm{4}{x}\int_{\mathrm{0}} ^{\infty} \frac{{e}^{{x}} }{\left(\mathrm{1}+{e}^{{x}} \right)^{\mathrm{2}} }{dx}−\int_{\mathrm{0}} ^{\infty} \mathrm{4}{x}\int\frac{{e}^{{x}} }{\left(\mathrm{1}+{e}^{{x}} \right)^{\mathrm{2}} } \\ $$$$=−\left[\frac{\mathrm{2}{x}}{\left(\mathrm{1}+{e}^{{x}} \right)}\right]_{\mathrm{0}} ^{\infty} +\mathrm{4}\int_{\mathrm{0}} ^{\infty} \frac{{x}}{\left(\mathrm{1}+{e}^{{x}} \right)}{dx} \\ $$$$=\mathrm{4}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \int_{\mathrm{0}} ^{\infty} {xe}^{−{nx}} {dx} \\ $$$$=\mathrm{4}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{\mathrm{1}}{{n}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} {ue}^{−{u}} {du} \\ $$$$=\mathrm{4}\overset{\infty} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}^{\mathrm{2}} }\Gamma\left(\mathrm{2}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}.\mathrm{4}=\frac{\pi^{\mathrm{2}} }{\mathrm{3}} \\ $$
Commented by mnjuly1970 last updated on 22/Nov/20

$${thank}\:{you}\:{mr} \\ $$$${payan}.. \\ $$
Answered by mathmax by abdo last updated on 22/Nov/20
![Ω =∫_(−∞) ^(+∞) (x^2 /((1+e^x )(1+e^(−x) )))dx changement e^(x ) =t give Ω =∫_0 ^∞ ((ln^2 t)/((1+t)(1+t^(−1) )))(dt/t) =∫_0 ^∞ ((ln^2 t)/((1+t)^2 ))dt =∫_0 ^1 ((ln^2 t)/((1+t)^2 ))dt +∫_1 ^∞ ((ln^2 t)/((1+t)^2 ))dt(→t=(1/x)) =2 ∫_0 ^1 ((ln^2 x)/((1+x)^2 ))dx we hsve for ∣x∣<1 (1/(1+x))=Σ_(n=0) ^∞ (−1)^n x^n ⇒ −(1/((1+x)^2 ))=Σ_(n=1) ^∞ n(−1)^n x^(n−1) =Σ_(n=0) ^∞ (n+1)(−1)^(n+1) x^n ⇒ (1/((1+x)^2 ))=Σ_(n=0) ^∞ (n+1)(−1)^n x^n ⇒ Ω =2 ∫_0 ^1 ln^2 x(Σ_(n=0) ^∞ (n+1)(−1)^n x^n )dx =2Σ_(n=0) ^∞ (n+1)(−1)^n ∫_0 ^1 x^n ln^2 x dx we have by parts ∫_0 ^1 x^n ln^2 xdx =[(x^(n+1) /(n+1))ln^2 x]_0 ^1 −∫_0 ^(1 ) (x^(n+1) /(n+1))((2lnx)/x)dx =−(2/(n+1))∫_0 ^1 x^(n ) lnx dx =−(2/(n+1)){[(x^(n+1) /(n+1))lnx]_0 ^1 −∫_0 ^1 (x^(n+1) /(n+1))(dx/x)} =(2/((n+1)^3 )) ⇒ Ω =2 Σ_(n=0) ^∞ (n+1)(−1)^n (2/((n+1)^3 )) =4 Σ_(n=0) ^∞ (((−1)^n )/((n+1)^2 )) =4 Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 ) =−4 Σ_(n=1) ^∞ (((−1)^n )/n^2 ) let δ(x)=Σ_(n=1) ^∞ (((−1)^n )/n^x ) we know δ(x) =(2^(1−x) −1)ξ(x) ⇒ δ(2)=Σ_(n=1) ^∞ (((−1)^n )/n^2 )=(2^(1−2) −1)ξ(2) =−(1/2).(π^2 /6)=−(π^2 /(12)) ⇒ Ω =−4×(−(π^2 /(12))) ⇒Ω =(π^2 /3)](https://www.tinkutara.com/question/Q123091.png)
$$\Omega\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{e}^{\mathrm{x}} \right)\left(\mathrm{1}+\mathrm{e}^{−\mathrm{x}} \right)}\mathrm{dx}\:\mathrm{changement}\:\mathrm{e}^{\mathrm{x}\:} =\mathrm{t}\:\mathrm{give} \\ $$$$\Omega\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{t}}{\left(\mathrm{1}+\mathrm{t}\right)\left(\mathrm{1}+\mathrm{t}^{−\mathrm{1}} \right)}\frac{\mathrm{dt}}{\mathrm{t}}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{t}}{\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{2}} }\mathrm{dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{t}}{\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{2}} }\mathrm{dt}\:+\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{t}}{\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{2}} }\mathrm{dt}\left(\rightarrow\mathrm{t}=\frac{\mathrm{1}}{\mathrm{x}}\right) \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{2}} }\mathrm{dx}\:\:\mathrm{we}\:\mathrm{hsve}\:\mathrm{for}\:\mid\mathrm{x}\mid<\mathrm{1}\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{n}} \:\Rightarrow \\ $$$$−\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{2}} }=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{n}−\mathrm{1}} \:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(\mathrm{n}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} \:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{2}} }=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(\mathrm{n}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{n}} \:\Rightarrow \\ $$$$\Omega\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{ln}^{\mathrm{2}} \mathrm{x}\left(\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(\mathrm{n}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{n}} \right)\mathrm{dx} \\ $$$$=\mathrm{2}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(\mathrm{n}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} \:\mathrm{ln}^{\mathrm{2}} \:\mathrm{x}\:\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{by}\:\mathrm{parts} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} \mathrm{ln}^{\mathrm{2}} \mathrm{xdx}\:=\left[\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\mathrm{ln}^{\mathrm{2}} \mathrm{x}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}\:} \frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\frac{\mathrm{2lnx}}{\mathrm{x}}\mathrm{dx} \\ $$$$=−\frac{\mathrm{2}}{\mathrm{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\mathrm{x}^{\mathrm{n}\:} \mathrm{lnx}\:\mathrm{dx}\:=−\frac{\mathrm{2}}{\mathrm{n}+\mathrm{1}}\left\{\left[\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\mathrm{lnx}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\frac{\mathrm{dx}}{\mathrm{x}}\right\} \\ $$$$=\frac{\mathrm{2}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{3}} }\:\Rightarrow\:\Omega\:=\mathrm{2}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(\mathrm{n}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{\mathrm{n}} \:\frac{\mathrm{2}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=\mathrm{4}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\mathrm{4}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}^{\mathrm{2}} }\:=−\mathrm{4}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} } \\ $$$$\mathrm{let}\:\delta\left(\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{x}} }\:\:\mathrm{we}\:\mathrm{know}\:\delta\left(\mathrm{x}\right)\:=\left(\mathrm{2}^{\mathrm{1}−\mathrm{x}} −\mathrm{1}\right)\xi\left(\mathrm{x}\right)\:\Rightarrow \\ $$$$\delta\left(\mathrm{2}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} }=\left(\mathrm{2}^{\mathrm{1}−\mathrm{2}} −\mathrm{1}\right)\xi\left(\mathrm{2}\right)\:=−\frac{\mathrm{1}}{\mathrm{2}}.\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:\Rightarrow \\ $$$$\Omega\:=−\mathrm{4}×\left(−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\right)\:\Rightarrow\Omega\:=\frac{\pi^{\mathrm{2}} }{\mathrm{3}} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 22/Nov/20
$${thank}\:{you}\:{so}\:{much}\:{sir}\:{max}. \\ $$
Commented by mathmax by abdo last updated on 23/Nov/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir} \\ $$
