Menu Close

nice-calculus-find-0-4-ln-x-4x-x-2-1-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 124432 by mnjuly1970 last updated on 03/Dec/20
... nice calculus... find:: φ=∫_0 ^( 4) ((ln(x))/((4x−x^2 )^(1/2) ))dx=?
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\:{nice}\:\:{calculus}… \\ $$$$\:\:\:\:{find}:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\phi=\int_{\mathrm{0}} ^{\:\mathrm{4}} \frac{{ln}\left({x}\right)}{\left(\mathrm{4}{x}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{dx}=? \\ $$
Answered by mindispower last updated on 03/Dec/20
x=4t q=∫_0 ^1 ((ln(4)+ln(t))/((t−t^2 )^(1/2) ))dt w=ln(4)∫_0 ^1 (1/(t^(1/2) (1−t)^(1/2) ))+∫_0 ^1 ((ln(t))/( (√t).(√(1−t))))dt =ln(4).∫_0 ^1 t^((1/2)−) (1−t)^((1/2)−1) dt+∂_c ∫_0 ^1 t^((1/2)+c−1) (1−t)^((1/2)−1) dt∣_(c=0) =ln(4)β((1/2),(1/2))+∂_C β((1/2)+c,(1/2))∣_(c=0) =((ln(4)π)/(sin((π/2))))+β((1/2)+c,(1/2))(Ψ((1/2)+c)−Ψ(1+c))∣_(c=0) =πln(4)+π(Ψ((1/2))−Ψ(1)) =π(ln(4)+π(−2ln(2)−γ+γ) =0
$${x}=\mathrm{4}{t} \\ $$$${q}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{4}\right)+{ln}\left({t}\right)}{\left({t}−{t}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{dt} \\ $$$${w}={ln}\left(\mathrm{4}\right)\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{t}^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−{t}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({t}\right)}{\:\sqrt{{t}}.\sqrt{\mathrm{1}−{t}}}{dt} \\ $$$$={ln}\left(\mathrm{4}\right).\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\frac{\mathrm{1}}{\mathrm{2}}−} \left(\mathrm{1}−{t}\right)^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} {dt}+\partial_{{c}} \int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\frac{\mathrm{1}}{\mathrm{2}}+{c}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} {dt}\mid_{{c}=\mathrm{0}} \\ $$$$={ln}\left(\mathrm{4}\right)\beta\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right)+\partial_{{C}} \beta\left(\frac{\mathrm{1}}{\mathrm{2}}+{c},\frac{\mathrm{1}}{\mathrm{2}}\right)\mid_{{c}=\mathrm{0}} \\ $$$$=\frac{{ln}\left(\mathrm{4}\right)\pi}{{sin}\left(\frac{\pi}{\mathrm{2}}\right)}+\beta\left(\frac{\mathrm{1}}{\mathrm{2}}+{c},\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}+{c}\right)−\Psi\left(\mathrm{1}+{c}\right)\right)\mid_{{c}=\mathrm{0}} \\ $$$$=\pi{ln}\left(\mathrm{4}\right)+\pi\left(\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\Psi\left(\mathrm{1}\right)\right) \\ $$$$ \\ $$$$=\pi\left({ln}\left(\mathrm{4}\right)+\pi\left(−\mathrm{2}{ln}\left(\mathrm{2}\right)−\gamma+\gamma\right)\right. \\ $$$$=\mathrm{0} \\ $$
Commented by mnjuly1970 last updated on 03/Dec/20
mercey mr mindspower.. thanks alot...
$${mercey}\:{mr}\:{mindspower}.. \\ $$$${thanks}\:{alot}… \\ $$
Commented by mindispower last updated on 05/Dec/20
withe pleasur sir
$${withe}\:{pleasur}\:{sir} \\ $$
Answered by mnjuly1970 last updated on 03/Dec/20
another way we know : ∫_0 ^( (π/2)) ln(sin(x))dx=((−π)/2)ln(2) ✓ x=4y φ=∫_0 ^( 1) ((ln(4)+ln(y))/( (√y) (√(1−y)))) dy =^(y=sin^2 (t)) ∫_0 ^( (π/2)) {((2ln(2)+2ln(sin(t))/(sin(t)cos(t)))}(2sin(t)cos(t))dt =2πln(2)+4∫_0 ^( (π/2)) ln(sin(t))dt =2πln(2)−2πln(2)=0✓
$${another}\:\:{way} \\ $$$${we}\:{know}\:: \\ $$$$\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {ln}\left({sin}\left({x}\right)\right){dx}=\frac{−\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:\checkmark \\ $$$$\:\:{x}=\mathrm{4}{y} \\ $$$$\:\:\:\phi=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}\left(\mathrm{4}\right)+{ln}\left({y}\right)}{\:\sqrt{{y}}\:\sqrt{\mathrm{1}−{y}}}\:{dy} \\ $$$$\:\:\:\:\:\overset{{y}={sin}^{\mathrm{2}} \left({t}\right)} {=}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \left\{\frac{\mathrm{2}{ln}\left(\mathrm{2}\right)+\mathrm{2}{ln}\left({sin}\left({t}\right)\right.}{{sin}\left({t}\right){cos}\left({t}\right)}\right\}\left(\mathrm{2}{sin}\left({t}\right){cos}\left({t}\right)\right){dt} \\ $$$$=\mathrm{2}\pi{ln}\left(\mathrm{2}\right)+\mathrm{4}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {ln}\left({sin}\left({t}\right)\right){dt} \\ $$$$\:=\mathrm{2}\pi{ln}\left(\mathrm{2}\right)−\mathrm{2}\pi{ln}\left(\mathrm{2}\right)=\mathrm{0}\checkmark \\ $$
Answered by mathmax by abdo last updated on 03/Dec/20
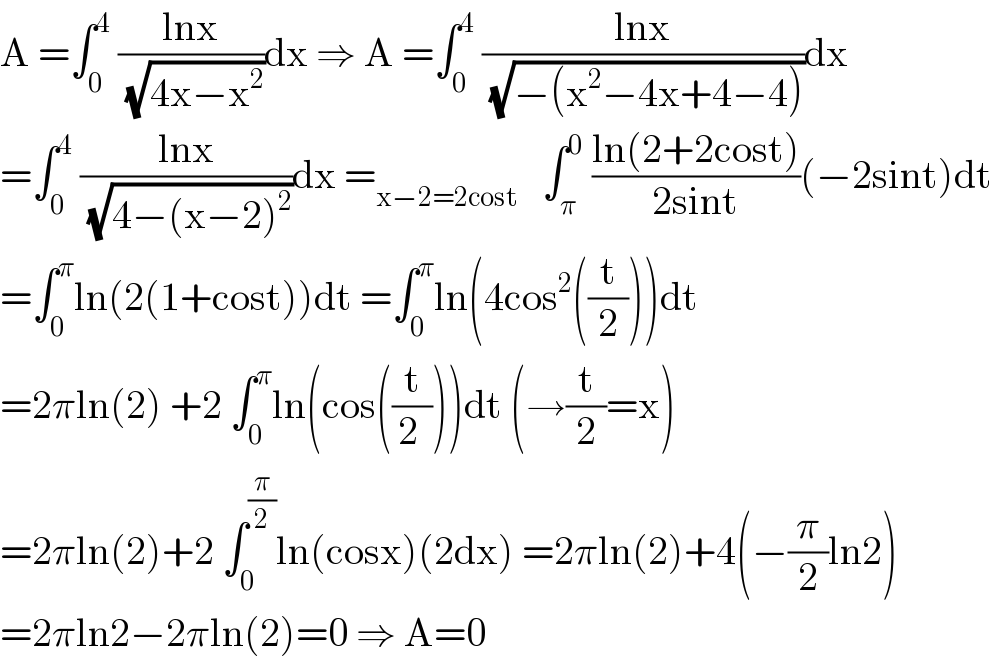
A =∫_0 ^4 ((lnx)/( (√(4x−x^2 ))))dx ⇒ A =∫_0 ^4 ((lnx)/( (√(−(x^2 −4x+4−4)))))dx =∫_0 ^4 ((lnx)/( (√(4−(x−2)^2 ))))dx =_(x−2=2cost) ∫_π ^0 ((ln(2+2cost))/(2sint))(−2sint)dt =∫_0 ^π ln(2(1+cost))dt =∫_0 ^π ln(4cos^2 ((t/2)))dt =2πln(2) +2 ∫_0 ^π ln(cos((t/(2 ))))dt (→(t/2)=x) =2πln(2)+2 ∫_0 ^(π/2) ln(cosx)(2dx) =2πln(2)+4(−(π/2)ln2) =2πln2−2πln(2)=0 ⇒ A=0
$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\mathrm{4}} \:\frac{\mathrm{lnx}}{\:\sqrt{\mathrm{4x}−\mathrm{x}^{\mathrm{2}} }}\mathrm{dx}\:\Rightarrow\:\mathrm{A}\:=\int_{\mathrm{0}} ^{\mathrm{4}} \:\frac{\mathrm{lnx}}{\:\sqrt{−\left(\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{4}−\mathrm{4}\right)}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{4}} \:\frac{\mathrm{lnx}}{\:\sqrt{\mathrm{4}−\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }}\mathrm{dx}\:=_{\mathrm{x}−\mathrm{2}=\mathrm{2cost}} \:\:\:\int_{\pi} ^{\mathrm{0}} \:\frac{\mathrm{ln}\left(\mathrm{2}+\mathrm{2cost}\right)}{\mathrm{2sint}}\left(−\mathrm{2sint}\right)\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\left(\mathrm{2}\left(\mathrm{1}+\mathrm{cost}\right)\right)\mathrm{dt}\:=\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\left(\mathrm{4cos}^{\mathrm{2}} \left(\frac{\mathrm{t}}{\mathrm{2}}\right)\right)\mathrm{dt} \\ $$$$=\mathrm{2}\pi\mathrm{ln}\left(\mathrm{2}\right)\:+\mathrm{2}\:\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\left(\mathrm{cos}\left(\frac{\mathrm{t}}{\mathrm{2}\:}\right)\right)\mathrm{dt}\:\left(\rightarrow\frac{\mathrm{t}}{\mathrm{2}}=\mathrm{x}\right) \\ $$$$=\mathrm{2}\pi\mathrm{ln}\left(\mathrm{2}\right)+\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{cosx}\right)\left(\mathrm{2dx}\right)\:=\mathrm{2}\pi\mathrm{ln}\left(\mathrm{2}\right)+\mathrm{4}\left(−\frac{\pi}{\mathrm{2}}\mathrm{ln2}\right) \\ $$$$=\mathrm{2}\pi\mathrm{ln2}−\mathrm{2}\pi\mathrm{ln}\left(\mathrm{2}\right)=\mathrm{0}\:\Rightarrow\:\mathrm{A}=\mathrm{0} \\ $$
Commented by mnjuly1970 last updated on 03/Dec/20
thanks alot sir max excellent
$${thanks}\:{alot}\:{sir}\:{max} \\ $$$${excellent} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *