Question Number 120156 by mnjuly1970 last updated on 29/Oct/20
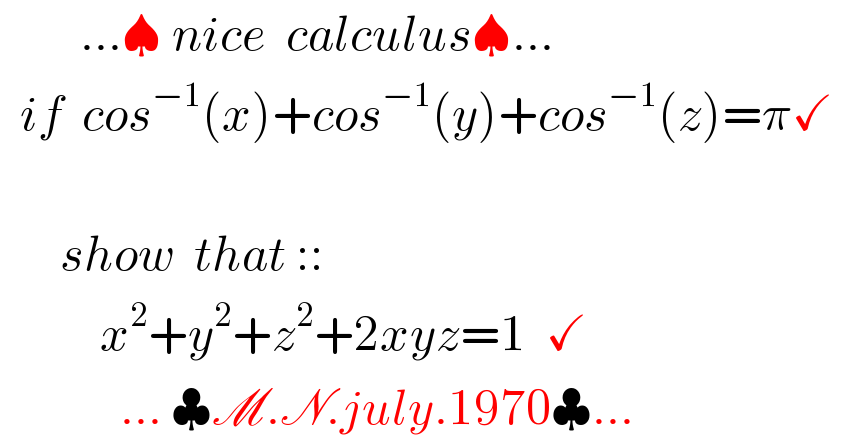
$$\:\:\:\:\:\:\:\:…\spadesuit\:{nice}\:\:{calculus}\spadesuit… \\ $$$$\:\:{if}\:\:{cos}^{−\mathrm{1}} \left({x}\right)+{cos}^{−\mathrm{1}} \left({y}\right)+{cos}^{−\mathrm{1}} \left({z}\right)=\pi\checkmark \\ $$$$ \\ $$$$\:\:\:\:\:\:{show}\:\:{that}\::: \\ $$$$\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} +\mathrm{2}{xyz}=\mathrm{1}\:\:\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:…\:\clubsuit\mathscr{M}.\mathscr{N}.{july}.\mathrm{1970}\clubsuit… \\ $$
Answered by TANMAY PANACEA last updated on 29/Oct/20
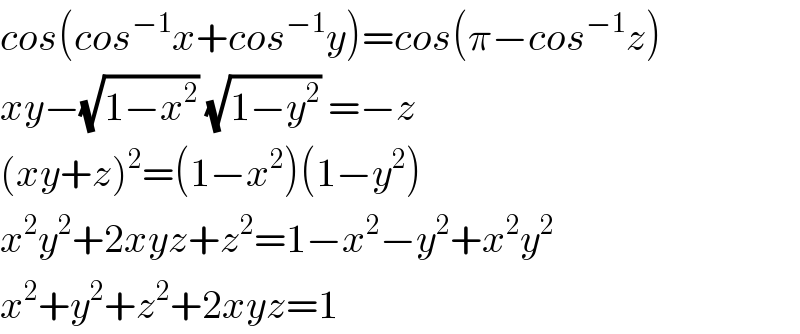
$${cos}\left({cos}^{−\mathrm{1}} {x}+{cos}^{−\mathrm{1}} {y}\right)={cos}\left(\pi−{cos}^{−\mathrm{1}} {z}\right) \\ $$$${xy}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }\:=−{z} \\ $$$$\left({xy}+{z}\right)^{\mathrm{2}} =\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\mathrm{1}−{y}^{\mathrm{2}} \right) \\ $$$${x}^{\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{2}{xyz}+{z}^{\mathrm{2}} =\mathrm{1}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} +{x}^{\mathrm{2}} {y}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} +\mathrm{2}{xyz}=\mathrm{1} \\ $$
Commented by mnjuly1970 last updated on 29/Oct/20
$${thank}\:{you}\:{so}\:{much}\:\:{master}\: \\ $$$${tanmay}…{grateful}… \\ $$
Commented by TANMAY PANACEA last updated on 29/Oct/20
$${most}\:{welcome}\:{sir} \\ $$
Commented by Dwaipayan Shikari last updated on 29/Oct/20
��
Commented by Ar Brandon last updated on 30/Oct/20
মহান কাজ��
Commented by Ar Brandon last updated on 30/Oct/20
ওহে, বন্ধু আমার. আশা করি ভালই আছ.��
Commented by som(math1967) last updated on 30/Oct/20
এসব কি?
Commented by Ar Brandon last updated on 30/Oct/20
কোথায় ? আপনি স্যার সম্পর্কে কি কথা বলছেন?��
Commented by som(math1967) last updated on 30/Oct/20

$$?? \\ $$
Commented by Dwaipayan Shikari last updated on 30/Oct/20
বাংলা শিখলে কখন?
Commented by Ar Brandon last updated on 30/Oct/20
কখনই না����
