Question Number 128680 by mnjuly1970 last updated on 09/Jan/21
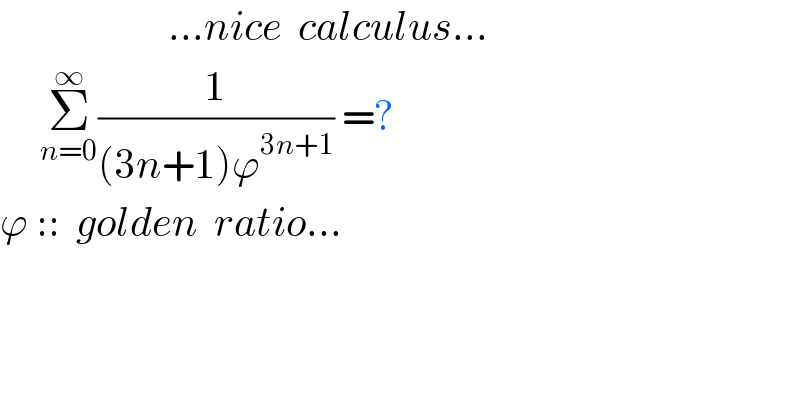
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…{nice}\:\:{calculus}… \\ $$$$\:\:\:\:\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)\varphi^{\mathrm{3}{n}+\mathrm{1}} }\:=? \\ $$$$\varphi\:::\:\:{golden}\:\:{ratio}… \\ $$$$ \\ $$
Answered by mr W last updated on 09/Jan/21
![Σ_(n=0) ^∞ x^(3n) =(1/(1−x^3 )) for ∣x∣<1 Σ_(n=0) ^∞ ∫_0 ^x x^(3n) dx=∫_0 ^x (1/(1−x^3 ))dx Σ_(n=0) ^∞ (x^(3n+1) /(3n+1))=−(1/3)∫_0 ^x ((1/(x−1))−((x+2)/(x^2 +x+1)))dx Σ_(n=0) ^∞ (x^(3n+1) /(3n+1))=[(1/6)ln ((x^2 +x+1)/((x−1)^2 ))+(1/( (√3)))tan^(−1) ((2x+1)/( (√3)))]_0 ^x Σ_(n=0) ^∞ (x^(3n+1) /(3n+1))=[(1/6)ln ((x^2 +x+1)/((x−1)^2 ))+(1/( (√3)))tan^(−1) ((2x+1)/( (√3)))−(π/(6(√3)))] x=(1/ϕ)=ϕ−1 x^2 =(1/ϕ^2 )=1−(1/ϕ)=2−ϕ ⇒Σ_(n=0) ^∞ (1/((3n+1)ϕ^(3n+1) ))=((ln 2)/6)+(2/3)ln ϕ+(1/( (√3)))tan^(−1) ((2ϕ−1)/( (√3)))−(π/(6(√3)))≈0.66042487](https://www.tinkutara.com/question/Q128683.png)
$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{\mathrm{3}{n}} =\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{3}} }\:{for}\:\mid{x}\mid<\mathrm{1} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{{x}} {x}^{\mathrm{3}{n}} {dx}=\int_{\mathrm{0}} ^{{x}} \frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{3}} }{dx} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{3}{n}+\mathrm{1}} }{\mathrm{3}{n}+\mathrm{1}}=−\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{{x}} \left(\frac{\mathrm{1}}{{x}−\mathrm{1}}−\frac{{x}+\mathrm{2}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\right){dx} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{3}{n}+\mathrm{1}} }{\mathrm{3}{n}+\mathrm{1}}=\left[\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\:\frac{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right]_{\mathrm{0}} ^{{x}} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{3}{n}+\mathrm{1}} }{\mathrm{3}{n}+\mathrm{1}}=\left[\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\:\frac{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}−\frac{\pi}{\mathrm{6}\sqrt{\mathrm{3}}}\right] \\ $$$${x}=\frac{\mathrm{1}}{\varphi}=\varphi−\mathrm{1} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{1}}{\varphi^{\mathrm{2}} }=\mathrm{1}−\frac{\mathrm{1}}{\varphi}=\mathrm{2}−\varphi \\ $$$$\Rightarrow\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)\varphi^{\mathrm{3}{n}+\mathrm{1}} }=\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{6}}+\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\:\varphi+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}\varphi−\mathrm{1}}{\:\sqrt{\mathrm{3}}}−\frac{\pi}{\mathrm{6}\sqrt{\mathrm{3}}}\approx\mathrm{0}.\mathrm{66042487} \\ $$
Commented by mnjuly1970 last updated on 09/Jan/21
$${thank}\:{you}\:{so}\:{much}\:{mrW} \\ $$$${grateful}… \\ $$
