Question Number 129805 by mnjuly1970 last updated on 19/Jan/21
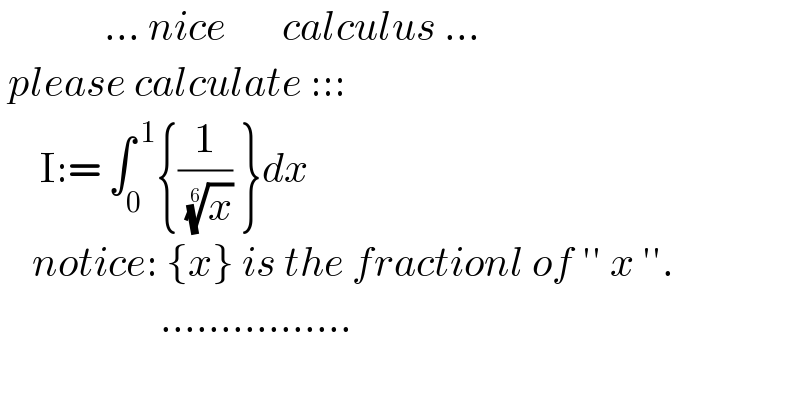
$$\:\:\:\:\:\:\:\:\:\:\:\:\:…\:{nice}\:\:\:\:\:\:\:{calculus}\:… \\ $$$$\:{please}\:{calculate}\:::: \\ $$$$\:\:\:\:\:\mathrm{I}:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \left\{\frac{\mathrm{1}}{\:\sqrt[{\mathrm{6}}]{{x}}}\:\right\}{dx} \\ $$$$\:\:\:\:{notice}:\:\left\{{x}\right\}\:{is}\:{the}\:{fractionl}\:{of}\:''\:{x}\:''. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:……………. \\ $$
Answered by mindispower last updated on 19/Jan/21
![let u=(1/(^6 (√x)))⇒x=(1/u^6 )⇒dx=((−6)/u^7 )du ⇔6∫_1 ^∞ {u}.(du/u^7 ) =6Σ_(k≥1) ∫_k ^(k+1) [u−k].(du/u^7 ) =6∫_1 ^∞ (du/u^6 )−6Σ_(k≥1) ∫_k ^(k+1) (k/u^7 )du =(6/5)+Σ_(k≥1) [(k/u^6 )]_k ^(k+1) =(6/5)+Σ_(k≥1) (k/((k+1)^6 ))−(1/k^5 ) =(6/5)+Σ_(k≥1) ((1/((k+1)^5 ))−(1/k^5 ))−(1/((k+1)^6 ))) =(6/5)−1−ζ(6)+1=(6/5)−ζ(6)=(6/5)−(π^6 /(945))](https://www.tinkutara.com/question/Q129823.png)
$${let}\:{u}=\frac{\mathrm{1}}{\:^{\mathrm{6}} \sqrt{{x}}}\Rightarrow{x}=\frac{\mathrm{1}}{{u}^{\mathrm{6}} }\Rightarrow{dx}=\frac{−\mathrm{6}}{{u}^{\mathrm{7}} }{du} \\ $$$$\Leftrightarrow\mathrm{6}\int_{\mathrm{1}} ^{\infty} \left\{{u}\right\}.\frac{{du}}{{u}^{\mathrm{7}} } \\ $$$$=\mathrm{6}\underset{{k}\geqslant\mathrm{1}} {\sum}\int_{{k}} ^{{k}+\mathrm{1}} \left[{u}−{k}\right].\frac{{du}}{{u}^{\mathrm{7}} } \\ $$$$=\mathrm{6}\int_{\mathrm{1}} ^{\infty} \frac{{du}}{{u}^{\mathrm{6}} }−\mathrm{6}\underset{{k}\geqslant\mathrm{1}} {\sum}\int_{{k}} ^{{k}+\mathrm{1}} \frac{{k}}{{u}^{\mathrm{7}} }{du} \\ $$$$=\frac{\mathrm{6}}{\mathrm{5}}+\underset{{k}\geqslant\mathrm{1}} {\sum}\left[\frac{{k}}{{u}^{\mathrm{6}} }\right]_{{k}} ^{{k}+\mathrm{1}} =\frac{\mathrm{6}}{\mathrm{5}}+\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{{k}}{\left({k}+\mathrm{1}\right)^{\mathrm{6}} }−\frac{\mathrm{1}}{{k}^{\mathrm{5}} } \\ $$$$\left.=\frac{\mathrm{6}}{\mathrm{5}}+\underset{{k}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)^{\mathrm{5}} }−\frac{\mathrm{1}}{{k}^{\mathrm{5}} }\right)−\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)^{\mathrm{6}} }\right) \\ $$$$=\frac{\mathrm{6}}{\mathrm{5}}−\mathrm{1}−\zeta\left(\mathrm{6}\right)+\mathrm{1}=\frac{\mathrm{6}}{\mathrm{5}}−\zeta\left(\mathrm{6}\right)=\frac{\mathrm{6}}{\mathrm{5}}−\frac{\pi^{\mathrm{6}} }{\mathrm{945}} \\ $$
