nice-calculus-prove-that-0-1-1-1-x-1-2-x-2-ln-1-x-dx-2-1-log-2-

Question Number 124064 by mnjuly1970 last updated on 30/Nov/20

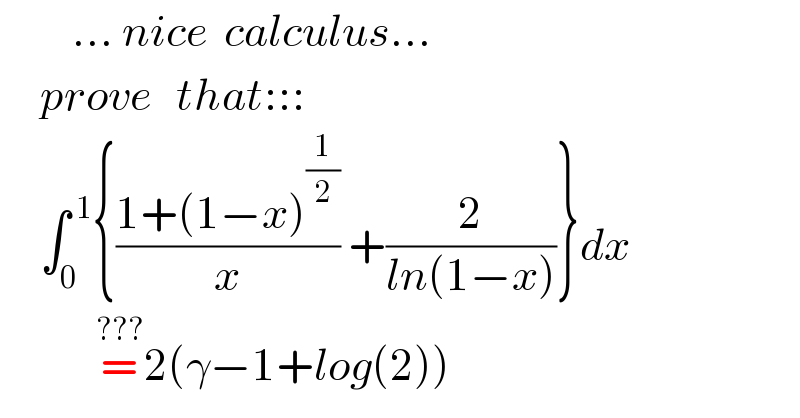
... nice calculus... prove that::: ∫_0 ^( 1) {((1+(1−x)^(1/2) )/x) +(2/(ln(1−x)))}dx =^(???) 2(γ−1+log(2))

$$\:\:\:\:\:\:\:\:\:…\:{nice}\:\:{calculus}… \\ $$$$\:\:\:\:\:{prove}\:\:\:{that}::: \\ $$$$\:\:\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \left\{\frac{\mathrm{1}+\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{{x}}\:+\frac{\mathrm{2}}{{ln}\left(\mathrm{1}−{x}\right)}\right\}{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\overset{???} {=}\mathrm{2}\left(\gamma−\mathrm{1}+{log}\left(\mathrm{2}\right)\right) \\ $$

Answered by mindispower last updated on 01/Dec/20

let ln(1−x)=−t ⇔∫_0 ^∞ {((1+e^(−(t/2)) )/(1−e^(−t) ))−(2/t)}e^(−t) dt =∫_0 ^∞ −((2e^(−t) )/t)+((1+e^(−(t/2)) )/(1−e^(−t) ))e^(−t) dt =−2∫{(e^(−t) /t)−(1/2)((1+e^(−(t/2)) )/(1−e^(−t) ))e^(−t) }dt =−2∫(e^(−t) /t)−(e^(−3(t/(2 ))) /(1−e^(−t) ))+(1/2).((e^(−(t/2)) −1)/(1−e^(−t) )).e^(−t) dt =−2∫_0 ^∞ {(e^(−t) /t)−(e^(−3(t/2)) /(1−e^(−t) ))}dt+∫_0 ^∞ ((1−e^(−(t/2)) )/(1−e^(−t) ))e^(−t) dt Ψ(z)=∫_0 ^∞ ((e^(−t) /t)−(e^(−zt) /(1−e^(−t) )))dt we get −2Ψ((3/2))+∫_0 ^∞ ((e^(−t) dt)/(1+e^(−(t/2)) ))=−2Ψ((3/2))+A A=∫_0 ^∞ {e^(−(t/2)) −1+(1/(1+e^(−(t/2)) ))}dt A=lim_(x→∞) ∫_0 ^x {e^(−(t/2)) −1+(1/(1+e^(−(t/2)) ))}dt =lim_(x→∞) [−2e^(−(x/2)) +2−x+2ln(e^(x/2) +1)−2ln(2)] =lim_(x→∞) [2−x+2.(x/2)+2ln(1+e^(−(x/2)) )−2ln(2)] =2−2ln(2) Ψ((3/2))=Ψ((1/2))+2=−2ln(2)−γ+2 we get −2(−2ln(2)−γ)+2−2ln(2) =2ln(2)+2γ−2=2(−1+γ+ln(2)) ∫((1+(√(1−x)))/x)+(2/(ln(1−x)))dx=2(γ−1+ln(2))

$${let}\:{ln}\left(\mathrm{1}−{x}\right)=−{t} \\ $$$$\Leftrightarrow\int_{\mathrm{0}} ^{\infty} \left\{\frac{\mathrm{1}+{e}^{−\frac{{t}}{\mathrm{2}}} }{\mathrm{1}−{e}^{−{t}} }−\frac{\mathrm{2}}{{t}}\right\}{e}^{−{t}} {dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} −\frac{\mathrm{2}{e}^{−{t}} }{{t}}+\frac{\mathrm{1}+{e}^{−\frac{{t}}{\mathrm{2}}} }{\mathrm{1}−{e}^{−{t}} }{e}^{−{t}} {dt} \\ $$$$=−\mathrm{2}\int\left\{\frac{{e}^{−{t}} }{{t}}−\frac{\mathrm{1}}{\mathrm{2}}\frac{\mathrm{1}+{e}^{−\frac{{t}}{\mathrm{2}}} }{\mathrm{1}−{e}^{−{t}} }{e}^{−{t}} \right\}{dt} \\ $$$$=−\mathrm{2}\int\frac{{e}^{−{t}} }{{t}}−\frac{{e}^{−\mathrm{3}\frac{{t}}{\mathrm{2}\:}} }{\mathrm{1}−{e}^{−{t}} }+\frac{\mathrm{1}}{\mathrm{2}}.\frac{{e}^{−\frac{{t}}{\mathrm{2}}} −\mathrm{1}}{\mathrm{1}−{e}^{−{t}} }.{e}^{−{t}} {dt} \\ $$$$=−\mathrm{2}\int_{\mathrm{0}} ^{\infty} \left\{\frac{{e}^{−{t}} }{{t}}−\frac{{e}^{−\mathrm{3}\frac{{t}}{\mathrm{2}}} }{\mathrm{1}−{e}^{−{t}} }\right\}{dt}+\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−{e}^{−\frac{{t}}{\mathrm{2}}} }{\mathrm{1}−{e}^{−{t}} }{e}^{−{t}} {dt} \\ $$$$\Psi\left({z}\right)=\int_{\mathrm{0}} ^{\infty} \left(\frac{{e}^{−{t}} }{{t}}−\frac{{e}^{−{zt}} }{\mathrm{1}−{e}^{−{t}} }\right){dt} \\ $$$${we}\:{get}\: \\ $$$$−\mathrm{2}\Psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)+\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{t}} {dt}}{\mathrm{1}+{e}^{−\frac{{t}}{\mathrm{2}}} }=−\mathrm{2}\Psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)+{A} \\ $$$${A}=\int_{\mathrm{0}} ^{\infty} \left\{{e}^{−\frac{{t}}{\mathrm{2}}} −\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+{e}^{−\frac{{t}}{\mathrm{2}}} }\right\}{dt} \\ $$$${A}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{{x}} \left\{{e}^{−\frac{{t}}{\mathrm{2}}} −\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+{e}^{−\frac{{t}}{\mathrm{2}}} }\right\}{dt} \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left[−\mathrm{2}{e}^{−\frac{{x}}{\mathrm{2}}} +\mathrm{2}−{x}+\mathrm{2}{ln}\left({e}^{\frac{{x}}{\mathrm{2}}} +\mathrm{1}\right)−\mathrm{2}{ln}\left(\mathrm{2}\right)\right] \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left[\mathrm{2}−{x}+\mathrm{2}.\frac{{x}}{\mathrm{2}}+\mathrm{2}{ln}\left(\mathrm{1}+{e}^{−\frac{{x}}{\mathrm{2}}} \right)−\mathrm{2}{ln}\left(\mathrm{2}\right)\right] \\ $$$$=\mathrm{2}−\mathrm{2}{ln}\left(\mathrm{2}\right) \\ $$$$\Psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{2}=−\mathrm{2}{ln}\left(\mathrm{2}\right)−\gamma+\mathrm{2} \\ $$$${we}\:{get}\:−\mathrm{2}\left(−\mathrm{2}{ln}\left(\mathrm{2}\right)−\gamma\right)+\mathrm{2}−\mathrm{2}{ln}\left(\mathrm{2}\right) \\ $$$$=\mathrm{2}{ln}\left(\mathrm{2}\right)+\mathrm{2}\gamma−\mathrm{2}=\mathrm{2}\left(−\mathrm{1}+\gamma+{ln}\left(\mathrm{2}\right)\right) \\ $$$$\int\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}}}{{x}}+\frac{\mathrm{2}}{{ln}\left(\mathrm{1}−{x}\right)}{dx}=\mathrm{2}\left(\gamma−\mathrm{1}+{ln}\left(\mathrm{2}\right)\right) \\ $$

Commented by mnjuly1970 last updated on 01/Dec/20

$${grateful}\:\:{sir}\:\:{mindspower}… \\ $$

Commented by mindispower last updated on 02/Dec/20

$${withe}\:{pleasur}\:{sir}\: \\ $$

Answered by mnjuly1970 last updated on 01/Dec/20

solution we know that .. i: ∫_0 ^( 1) ((1/(ln(x)))+(1/(1−x)))dx=_([IMAGE⇓⇓]) ^(why?) γ ✓ ii:∫_0 ^( 1) ((t^n −1)/(ln(t)))dt=^(why?) ln(n+1) ✓ Φ=∫_0 ^( 1) (((1+(√(1−x)))/x)+(2/(ln(1−x))))dx =^(1−x=t^2 ) 2∫_0 ^( 1) {((1+t)/(1−t^2 ))+(2/(2ln(t)))}tdt =2∫_0 ^( 1) ((1/(1−t))+(1/(ln(t))))tdt =2∫_0 ^( 1) (((t−1+1)/(1−t))+((t+1−1)/(ln(t))))dt =2∫_0 ^( 1) ((1/(1−t))+(1/(ln(t))))dt−2+∫_0 ^( 1) ((t^1 −1)/(ln(t)))dt =2γ−2+ln(2)=2(γ−1+ln(2))✓

$${solution} \\ $$$$\:\:{we}\:{know}\:{that}\:\:.. \\ $$$$\:\:\:{i}:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{\mathrm{1}}{{ln}\left({x}\right)}+\frac{\mathrm{1}}{\mathrm{1}−{x}}\right){dx}\underset{\left[{IMAGE}\Downarrow\Downarrow\right]} {\overset{{why}?} {=}}\:\gamma\:\checkmark \\ $$$$\:\:\:{ii}:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{t}^{{n}} −\mathrm{1}}{{ln}\left({t}\right)}{dt}\overset{{why}?} {=}{ln}\left({n}+\mathrm{1}\right)\:\checkmark \\ $$$$\:\:\:\Phi=\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}}}{{x}}+\frac{\mathrm{2}}{{ln}\left(\mathrm{1}−{x}\right)}\right){dx} \\ $$$$\overset{\mathrm{1}−{x}={t}^{\mathrm{2}} } {=}\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \left\{\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{2}{ln}\left({t}\right)}\right\}{tdt}\: \\ $$$$\:\:\:\:\:=\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{1}−{t}}+\frac{\mathrm{1}}{{ln}\left({t}\right)}\right){tdt} \\ $$$$\:\:\:\:\:\:=\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{{t}−\mathrm{1}+\mathrm{1}}{\mathrm{1}−{t}}+\frac{{t}+\mathrm{1}−\mathrm{1}}{{ln}\left({t}\right)}\right){dt} \\ $$$$\:\:\:\:\:\:=\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{1}−{t}}+\frac{\mathrm{1}}{{ln}\left({t}\right)}\right){dt}−\mathrm{2}+\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{t}^{\mathrm{1}} −\mathrm{1}}{{ln}\left({t}\right)}{dt} \\ $$$$\:\:\:\:=\mathrm{2}\gamma−\mathrm{2}+{ln}\left(\mathrm{2}\right)=\mathrm{2}\left(\gamma−\mathrm{1}+{ln}\left(\mathrm{2}\right)\right)\checkmark \\ $$$$\:\:\:\:\:\:\: \\ $$

Commented by mnjuly1970 last updated on 01/Dec/20