Question Number 122035 by mnjuly1970 last updated on 13/Nov/20
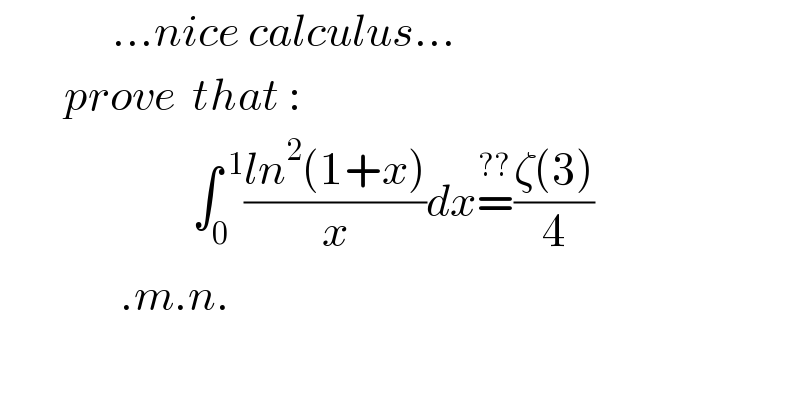
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:…{nice}\:{calculus}… \\ $$$$\:\:\:\:\:\:\:\:{prove}\:\:{that}\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)}{{x}}{dx}\overset{??} {=}\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:.{m}.{n}. \\ $$
Answered by mindispower last updated on 14/Nov/20
![∫u^2 e^(−u) −u^2 e^(−u) −2ue^(−u) −2e^(−u) ∫_0 ^(ln(2)) (u^2 /(e^u −1))e^u du =∫_0 ^(ln(2)) Σ_(n≥0) u^2 e^(−nu) du=((ln^3 (2))/3) +Σ_(n≥1) ∫_0 ^(ln(2)) u^2 e^(−nu) du=Σ_(n≥1) (1/n^3 )∫_0 ^(nln(2)) x^2 e^(−x) dx =((ln^3 (2))/3)+Σ_(n≥1) (1/n^3 )[−x^2 e^(−x) −2xe^(−x) −2e^(−x) ]_0 ^(nln(2)) =((ln^3 (2))/3)+Σ_(n≥1) [−n^2 ln^2 (2).(1/2^n )−((2nln(2))/2^n )−2.(1/2^n )+2].(1/n^3 ) =((ln^3 (2))/3)−ln^2 (2)Σ_(n≥1) (1/(n.2^n ))−2ln(2)Σ_(n≥1) (1/(n^2 2^n ))−2Σ_(n≥1) (1/(n^3 2^n ))+2ζ(3) =−((2ln^3 (2))/3)−2ln(2)Li_2 ((1/2))−2Li_3 ((1/2))+2ζ(3) −2((ln^3 (2))/3)−2ln(2)((π^2 /(12))−(1/2)ln^2 (2))−2(((ln^3 (2))/6)−((π^2 ln(2))/(12))+(7/8)ζ(3))+2ζ(3) =−(7/4)ζ(3)+2ζ(3)=(1/4)ζ(3) Li_2 ((1/2))=(π^2 /(12))−((ln^2 (2))/2),Li_3 ((1/2))=((ln^3 (2))/6)−((π^2 ln(2))/(12))+((7ζ(3))/8)](https://www.tinkutara.com/question/Q122077.png)
$$\int{u}^{\mathrm{2}} {e}^{−{u}} \\ $$$$−{u}^{\mathrm{2}} {e}^{−{u}} −\mathrm{2}{ue}^{−{u}} −\mathrm{2}{e}^{−{u}} \\ $$$$\int_{\mathrm{0}} ^{{ln}\left(\mathrm{2}\right)} \frac{{u}^{\mathrm{2}} }{{e}^{{u}} −\mathrm{1}}{e}^{{u}} {du} \\ $$$$=\int_{\mathrm{0}} ^{{ln}\left(\mathrm{2}\right)} \underset{{n}\geqslant\mathrm{0}} {\sum}{u}^{\mathrm{2}} {e}^{−{nu}} {du}=\frac{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{3}} \\ $$$$+\underset{{n}\geqslant\mathrm{1}} {\sum}\int_{\mathrm{0}} ^{{ln}\left(\mathrm{2}\right)} {u}^{\mathrm{2}} {e}^{−{nu}} {du}=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\int_{\mathrm{0}} ^{{nln}\left(\mathrm{2}\right)} {x}^{\mathrm{2}} {e}^{−{x}} {dx} \\ $$$$=\frac{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{3}}+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\left[−{x}^{\mathrm{2}} {e}^{−{x}} −\mathrm{2}{xe}^{−{x}} −\mathrm{2}{e}^{−{x}} \right]_{\mathrm{0}} ^{{nln}\left(\mathrm{2}\right)} \\ $$$$=\frac{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{3}}+\underset{{n}\geqslant\mathrm{1}} {\sum}\left[−{n}^{\mathrm{2}} {ln}^{\mathrm{2}} \left(\mathrm{2}\right).\frac{\mathrm{1}}{\mathrm{2}^{{n}} }−\frac{\mathrm{2}{nln}\left(\mathrm{2}\right)}{\mathrm{2}^{{n}} }−\mathrm{2}.\frac{\mathrm{1}}{\mathrm{2}^{{n}} }+\mathrm{2}\right].\frac{\mathrm{1}}{{n}^{\mathrm{3}} } \\ $$$$=\frac{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{3}}−{ln}^{\mathrm{2}} \left(\mathrm{2}\right)\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}.\mathrm{2}^{{n}} }−\mathrm{2}{ln}\left(\mathrm{2}\right)\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}^{\mathrm{2}} \mathrm{2}^{{n}} }−\mathrm{2}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}^{\mathrm{3}} \mathrm{2}^{{n}} }+\mathrm{2}\zeta\left(\mathrm{3}\right) \\ $$$$=−\frac{\mathrm{2}{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{3}}−\mathrm{2}{ln}\left(\mathrm{2}\right){Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{2}{Li}_{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{2}\zeta\left(\mathrm{3}\right) \\ $$$$−\mathrm{2}\frac{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{3}}−\mathrm{2}{ln}\left(\mathrm{2}\right)\left(\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\frac{\mathrm{1}}{\mathrm{2}}{ln}^{\mathrm{2}} \left(\mathrm{2}\right)\right)−\mathrm{2}\left(\frac{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{6}}−\frac{\pi^{\mathrm{2}} {ln}\left(\mathrm{2}\right)}{\mathrm{12}}+\frac{\mathrm{7}}{\mathrm{8}}\zeta\left(\mathrm{3}\right)\right)+\mathrm{2}\zeta\left(\mathrm{3}\right) \\ $$$$=−\frac{\mathrm{7}}{\mathrm{4}}\zeta\left(\mathrm{3}\right)+\mathrm{2}\zeta\left(\mathrm{3}\right)=\frac{\mathrm{1}}{\mathrm{4}}\zeta\left(\mathrm{3}\right) \\ $$$${Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}},{Li}_{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{6}}−\frac{\pi^{\mathrm{2}} {ln}\left(\mathrm{2}\right)}{\mathrm{12}}+\frac{\mathrm{7}\zeta\left(\mathrm{3}\right)}{\mathrm{8}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 14/Nov/20
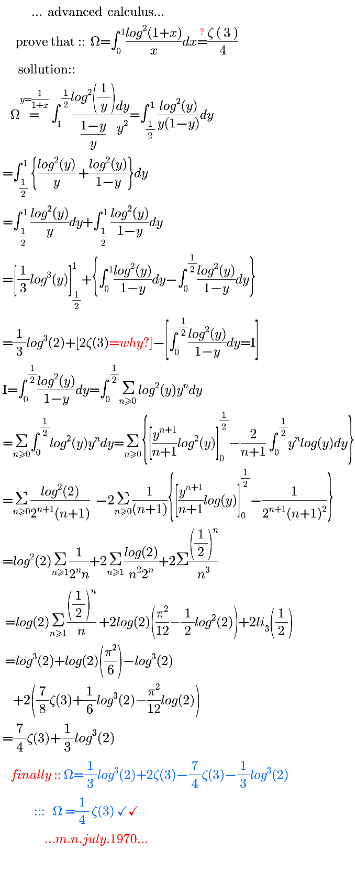
Commented by mnjuly1970 last updated on 14/Nov/20
$${thank}\:{you}\:{mr}\:{power} \\ $$
Commented by mindispower last updated on 14/Nov/20
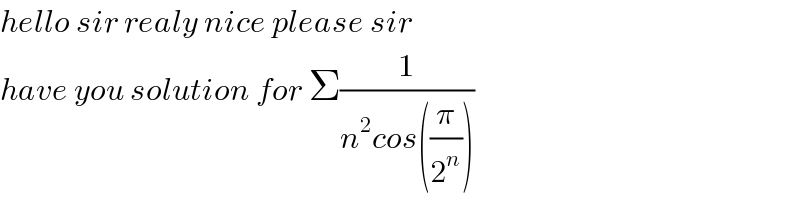
$${hello}\:{sir}\:{realy}\:{nice}\:{please}\:{sir} \\ $$$${have}\:{you}\:{solution}\:{for}\:\Sigma\frac{\mathrm{1}}{{n}^{\mathrm{2}} {cos}\left(\frac{\pi}{\mathrm{2}^{{n}} }\right)} \\ $$
