Question Number 123387 by mnjuly1970 last updated on 25/Nov/20
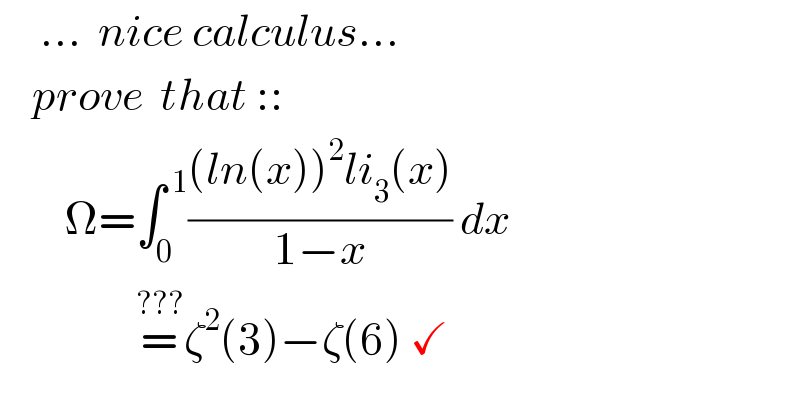
$$\:\:\:\:\:…\:\:{nice}\:{calculus}… \\ $$$$\:\:\:\:{prove}\:\:{that}\::: \\ $$$$\:\:\:\:\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left({ln}\left({x}\right)\right)^{\mathrm{2}} {li}_{\mathrm{3}} \left({x}\right)}{\mathrm{1}−{x}}\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\overset{???} {=}\zeta^{\mathrm{2}} \left(\mathrm{3}\right)−\zeta\left(\mathrm{6}\right)\:\checkmark \\ $$
Commented by talminator2856791 last updated on 25/Nov/20

$$\:\mathrm{what}\:\mathrm{is}\:\mathrm{li}_{\mathrm{3}} ? \\ $$
Commented by mnjuly1970 last updated on 25/Nov/20

$$\:{li}_{\mathrm{3}} \left({x}\right)\:=\int_{\mathrm{0}} ^{\:{x}} \frac{{li}_{\mathrm{2}} \left({t}\right)}{{t}}{dt}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}^{\mathrm{3}} } \\ $$$$\:\:\:{trilogarithm}\:{function}. \\ $$$$\:\:\:{li}_{{z}} \left({x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}^{{z}} } \\ $$$${example}:\:{li}_{\mathrm{2}} \left(\mathrm{1}\right)=\zeta\left(\mathrm{2}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\:{li}_{\mathrm{3}} \left(\mathrm{1}\right)=\zeta\left(\mathrm{3}\right)\:\:,\:{li}_{\mathrm{2}} \left(−\mathrm{1}\right)=−\eta\left(\mathrm{2}\right)=−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\: \\ $$$$,…. \\ $$
