Question Number 122882 by mnjuly1970 last updated on 20/Nov/20
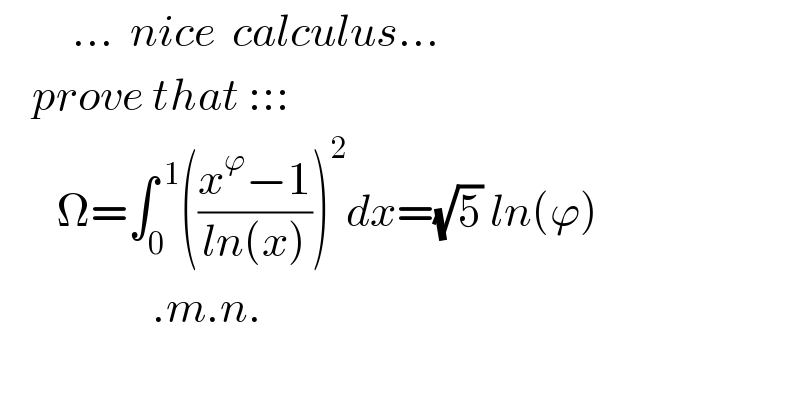
$$\:\:\:\:\:\:\:\:\:…\:\:{nice}\:\:{calculus}… \\ $$$$\:\:\:\:{prove}\:{that}\:::: \\ $$$$\:\:\:\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{{x}^{\varphi} −\mathrm{1}}{{ln}\left({x}\right)}\right)^{\mathrm{2}} {dx}=\sqrt{\mathrm{5}}\:{ln}\left(\varphi\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:.{m}.{n}. \\ $$
Answered by TANMAY PANACEA last updated on 20/Nov/20
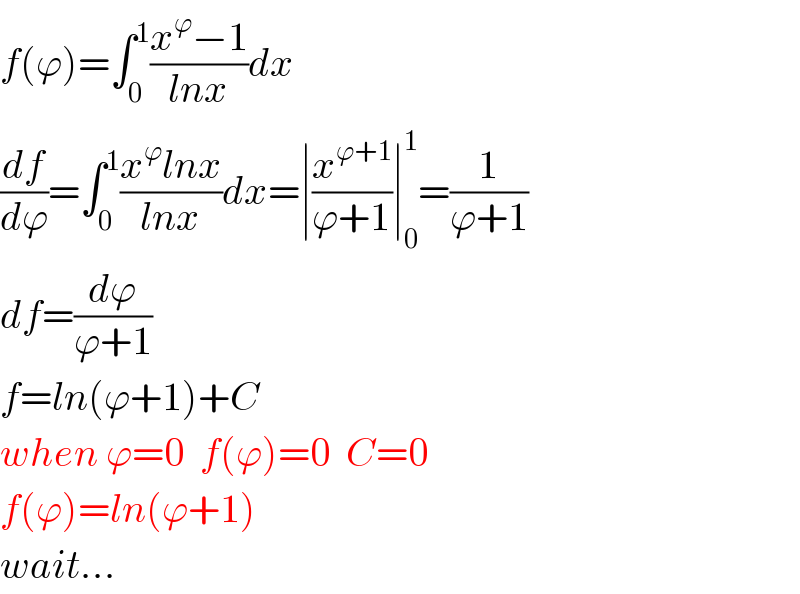
$${f}\left(\varphi\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\varphi} −\mathrm{1}}{{lnx}}{dx} \\ $$$$\frac{{df}}{{d}\varphi}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\varphi} {lnx}}{{lnx}}{dx}=\mid\frac{{x}^{\varphi+\mathrm{1}} }{\varphi+\mathrm{1}}\mid_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{1}}{\varphi+\mathrm{1}} \\ $$$${df}=\frac{{d}\varphi}{\varphi+\mathrm{1}} \\ $$$${f}={ln}\left(\varphi+\mathrm{1}\right)+{C} \\ $$$${when}\:\varphi=\mathrm{0}\:\:{f}\left(\varphi\right)=\mathrm{0}\:\:{C}=\mathrm{0} \\ $$$${f}\left(\varphi\right)={ln}\left(\varphi+\mathrm{1}\right) \\ $$$${wait}… \\ $$
Commented by mnjuly1970 last updated on 21/Nov/20
![thank you mr tanmay for your effort with your permission i present the solution. note :ln(N)=∫_0 ^( 1) ((x^(N−1) −1)/(ln(x)))dx f(a)=∫_0 ^( 1) (((x^a −1)^2 )/(ln^2 (x)))dx f ′(a)=∫_0 ^( 1) (∂/∂a)[(((x^a −1)^2 )/(ln^2 (x)))] =∫_0 ^( 1) ((2(x^a −1)x^a ln(x))/(ln^2 (x)))dx=2∫_0 ^( 1) ((x^(2a) −x^a )/(ln(x)))dx =2∫_0 ^( 1) ((x^(2a) −1)/(ln(x))) +2∫_0 ^( 1) ((1−x^a )/(ln(x)))dx =2ln(2a+1)−2ln(a+1) f(a)=2∫^ ln(2a+1)da−2∫ln(a+1)da+C =(2a+1)ln(2a+1)−(2a+1) −2(a+1)ln(a+1)+2(a+1)+C f(0)=1+C⇒C=−1 f(a)=(2a+1)ln(2a+1)−2(a+1)ln(a+1)+1−1 Ω=f(ϕ)=(2ϕ+1)ln(2ϕ+1)−2(ϕ+1)ln(ϕ+1) ϕ: is golden ratio and we know: ϕ^2 =ϕ+1 =(ϕ^2 +ϕ)ln(ϕ^2 +ϕ)−2ϕ^2 ln(ϕ^2 ) =ϕ^3 ln(ϕ^3 )−4ϕ^2 ln(ϕ) =(3ϕ^3 −4ϕ^2 )ln(ϕ)=(3ϕ^2 +3ϕ−4ϕ^2 )ln(ϕ) =(−ϕ^2 +3ϕ)ln(ϕ)=(−ϕ−1+3ϕ)ln(ϕ) =(2ϕ−1)ln(ϕ)=(2(((1+(√5))/2))−1)ln(ϕ) =(√5) ln(ϕ) ✓ ✓✓](https://www.tinkutara.com/question/Q122972.png)
$${thank}\:{you}\:{mr}\:{tanmay}\:{for}\:{your} \\ $$$${effort}\: \\ $$$${with}\:{your}\:{permission} \\ $$$$\:{i}\:{present}\:{the}\:{solution}. \\ $$$${note}\::{ln}\left({N}\right)=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}^{{N}−\mathrm{1}} −\mathrm{1}}{{ln}\left({x}\right)}{dx} \\ $$$$\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left({x}^{{a}} −\mathrm{1}\right)^{\mathrm{2}} }{{ln}^{\mathrm{2}} \left({x}\right)}{dx} \\ $$$$\:{f}\:'\left({a}\right)=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\partial}{\partial{a}}\left[\frac{\left({x}^{{a}} −\mathrm{1}\right)^{\mathrm{2}} }{{ln}^{\mathrm{2}} \left({x}\right)}\right] \\ $$$$=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{2}\left({x}^{{a}} −\mathrm{1}\right){x}^{{a}} {ln}\left({x}\right)}{{ln}^{\mathrm{2}} \left({x}\right)}{dx}=\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}^{\mathrm{2}{a}} −{x}^{{a}} }{{ln}\left({x}\right)}{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}^{\mathrm{2}{a}} −\mathrm{1}}{{ln}\left({x}\right)}\:+\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}−{x}^{{a}} }{{ln}\left({x}\right)}{dx} \\ $$$$=\mathrm{2}{ln}\left(\mathrm{2}{a}+\mathrm{1}\right)−\mathrm{2}{ln}\left({a}+\mathrm{1}\right) \\ $$$${f}\left({a}\right)=\mathrm{2}\int^{\:} {ln}\left(\mathrm{2}{a}+\mathrm{1}\right){da}−\mathrm{2}\int{ln}\left({a}+\mathrm{1}\right){da}+{C} \\ $$$$=\left(\mathrm{2}{a}+\mathrm{1}\right){ln}\left(\mathrm{2}{a}+\mathrm{1}\right)−\left(\mathrm{2}{a}+\mathrm{1}\right) \\ $$$$\:\:\:−\mathrm{2}\left({a}+\mathrm{1}\right){ln}\left({a}+\mathrm{1}\right)+\mathrm{2}\left({a}+\mathrm{1}\right)+{C} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{1}+{C}\Rightarrow{C}=−\mathrm{1} \\ $$$${f}\left({a}\right)=\left(\mathrm{2}{a}+\mathrm{1}\right){ln}\left(\mathrm{2}{a}+\mathrm{1}\right)−\mathrm{2}\left({a}+\mathrm{1}\right){ln}\left({a}+\mathrm{1}\right)+\mathrm{1}−\mathrm{1} \\ $$$$\:\: \\ $$$$\Omega={f}\left(\varphi\right)=\left(\mathrm{2}\varphi+\mathrm{1}\right){ln}\left(\mathrm{2}\varphi+\mathrm{1}\right)−\mathrm{2}\left(\varphi+\mathrm{1}\right){ln}\left(\varphi+\mathrm{1}\right) \\ $$$$\:\:\varphi:\:{is}\:{golden}\:{ratio} \\ $$$$\:\:\:{and}\:\:{we}\:{know}:\:\varphi^{\mathrm{2}} =\varphi+\mathrm{1} \\ $$$$=\left(\varphi^{\mathrm{2}} +\varphi\right){ln}\left(\varphi^{\mathrm{2}} +\varphi\right)−\mathrm{2}\varphi^{\mathrm{2}} {ln}\left(\varphi^{\mathrm{2}} \right) \\ $$$$=\varphi^{\mathrm{3}} {ln}\left(\varphi^{\mathrm{3}} \right)−\mathrm{4}\varphi^{\mathrm{2}} {ln}\left(\varphi\right) \\ $$$$=\left(\mathrm{3}\varphi^{\mathrm{3}} −\mathrm{4}\varphi^{\mathrm{2}} \right){ln}\left(\varphi\right)=\left(\mathrm{3}\varphi^{\mathrm{2}} +\mathrm{3}\varphi−\mathrm{4}\varphi^{\mathrm{2}} \right){ln}\left(\varphi\right) \\ $$$$=\left(−\varphi^{\mathrm{2}} +\mathrm{3}\varphi\right){ln}\left(\varphi\right)=\left(−\varphi−\mathrm{1}+\mathrm{3}\varphi\right){ln}\left(\varphi\right) \\ $$$$\:=\left(\mathrm{2}\varphi−\mathrm{1}\right){ln}\left(\varphi\right)=\left(\mathrm{2}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)−\mathrm{1}\right){ln}\left(\varphi\right) \\ $$$$=\sqrt{\mathrm{5}}\:{ln}\left(\varphi\right)\:\:\checkmark\:\checkmark\checkmark \\ $$
