Menu Close

nice-calculus-prove-that-0-x-x-1-x-4-x-4-dx-2-1-4-pi-is-Golden-ratio-

Tinku Tara 0 Comments
Pin




Question Number 123961 by mnjuly1970 last updated on 29/Nov/20
...nice calculus... prove that:: Ω= ∫_0 ^( ∞) ((x^ϕ /((x+1)(√(x^(4ϕ) +x^4 )))))dx =^(???) ((ϕΓ^2 ((1/4)))/( (√π))) ϕ is Golden ratio ...
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…{nice}\:\:\:{calculus}… \\ $$$$\:\:{prove}\:\:{that}:: \\ $$$$ \\ $$$$\:\:\:\:\Omega=\:\int_{\mathrm{0}} ^{\:\infty} \left(\frac{{x}^{\varphi} }{\left({x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{4}\varphi} +{x}^{\mathrm{4}} }}\right){dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\overset{???} {=}\:\frac{\varphi\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\:\sqrt{\pi}} \\ $$$$\:\:\:\:\:\:\:\:\varphi\:{is}\:\:{Golden}\:{ratio}\:… \\ $$
Answered by mindispower last updated on 29/Nov/20
2Ω=∫_0 ^∞ (x^ϕ /((1+x)(√(x^(4ϕ) +x^4 ))))+(1/x^ϕ ).(dx/(x^2 (1+(1/x))(√((x^(4ϕ) +x^4 )/x^(4ϕ+4) )))) =∫_0 ^∞ ((x^ϕ +x^(ϕ+1) )/((x+1)(√(x^4 +x^(4ϕ) ))))dx=∫(x^ϕ /( (√(x^4 +x^(4ϕ) )))) =∫_0 ^∞ (x^(ϕ−2) /( (√(1+x^(4(ϕ−1)) ))))dx let x^((ϕ−1)) =t⇒x^(ϕ−2) dx=(dt/(ϕ−1)) =∫_0 ^∞ (dt/((ϕ−1)(√(1+t^4 )))) t=(√(tg(r)))⇒dt=(dx/(2cos^(3/2) (x)sin^(1/2) )) Ω=_ (1/(2(ϕ−1)))∫_0 ^(π/2) ((cos(x)dx)/(cos^(3/2) (x)sin^(1/2) (x))) Ω=(1/4).2∫_0 ^(π/2) cos^(2((1/4))−1) (x)sin^(2((1/4))−1) (x)dx =(1/(4(ϕ−1)))β((1/4),(1/4))=(1/(4(ϕ−1)))((Γ^2 ((1/4)))/(Γ((1/2))))=((Γ^2 ((1/4)))/(4(√π)(ϕ−1))) ϕ^2 −ϕ−1=0=ϕ(ϕ−1)−1⇒(1/(ϕ−1))=ϕ 2Ω=((ϕΓ^2 ((1/4)))/(4(√π))),Ω=(ϕ/(8(√π)))Γ^2 ((1/4))
$$\mathrm{2}\Omega=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\varphi} }{\left(\mathrm{1}+{x}\right)\sqrt{{x}^{\mathrm{4}\varphi} +{x}^{\mathrm{4}} }}+\frac{\mathrm{1}}{{x}^{\varphi} }.\frac{{dx}}{{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\sqrt{\frac{{x}^{\mathrm{4}\varphi} +{x}^{\mathrm{4}} }{{x}^{\mathrm{4}\varphi+\mathrm{4}} }}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\varphi} +{x}^{\varphi+\mathrm{1}} }{\left({x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{4}\varphi} }}{dx}=\int\frac{{x}^{\varphi} }{\:\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{4}\varphi} }} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\varphi−\mathrm{2}} }{\:\sqrt{\mathrm{1}+{x}^{\mathrm{4}\left(\varphi−\mathrm{1}\right)} }}{dx} \\ $$$${let}\:{x}^{\left(\varphi−\mathrm{1}\right)} \:={t}\Rightarrow{x}^{\varphi−\mathrm{2}} {dx}=\frac{{dt}}{\varphi−\mathrm{1}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\left(\varphi−\mathrm{1}\right)\sqrt{\mathrm{1}+{t}^{\mathrm{4}} }} \\ $$$${t}=\sqrt{{tg}\left({r}\right)}\Rightarrow{dt}=\frac{{dx}}{\mathrm{2}{cos}^{\frac{\mathrm{3}}{\mathrm{2}}} \left({x}\right){sin}^{\frac{\mathrm{1}}{\mathrm{2}}} } \\ $$$$\Omega=_{} \frac{\mathrm{1}}{\mathrm{2}\left(\varphi−\mathrm{1}\right)}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cos}\left({x}\right){dx}}{{cos}^{\frac{\mathrm{3}}{\mathrm{2}}} \left({x}\right){sin}^{\frac{\mathrm{1}}{\mathrm{2}}} \left({x}\right)} \\ $$$$\Omega=\frac{\mathrm{1}}{\mathrm{4}}.\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)−\mathrm{1}} \left({x}\right){sin}^{\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)−\mathrm{1}} \left({x}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\left(\varphi−\mathrm{1}\right)}\beta\left(\frac{\mathrm{1}}{\mathrm{4}},\frac{\mathrm{1}}{\mathrm{4}}\right)=\frac{\mathrm{1}}{\mathrm{4}\left(\varphi−\mathrm{1}\right)}\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}=\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\mathrm{4}\sqrt{\pi}\left(\varphi−\mathrm{1}\right)} \\ $$$$\varphi^{\mathrm{2}} −\varphi−\mathrm{1}=\mathrm{0}=\varphi\left(\varphi−\mathrm{1}\right)−\mathrm{1}\Rightarrow\frac{\mathrm{1}}{\varphi−\mathrm{1}}=\varphi \\ $$$$\mathrm{2}\Omega=\frac{\varphi\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\mathrm{4}\sqrt{\pi}},\Omega=\frac{\varphi}{\mathrm{8}\sqrt{\pi}}\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 29/Nov/20
thank you master mindspower excellent as always..
$$\:\:{thank}\:{you}\:{master}\:{mindspower} \\ $$$${excellent}\:{as}\:{always}.. \\ $$
Commented by mindispower last updated on 02/Dec/20
withe plessur sir have a nice day
$${withe}\:{plessur}\:{sir}\:{have}\:{a}\:{nice}\:{day} \\ $$
Answered by Dwaipayan Shikari last updated on 29/Nov/20
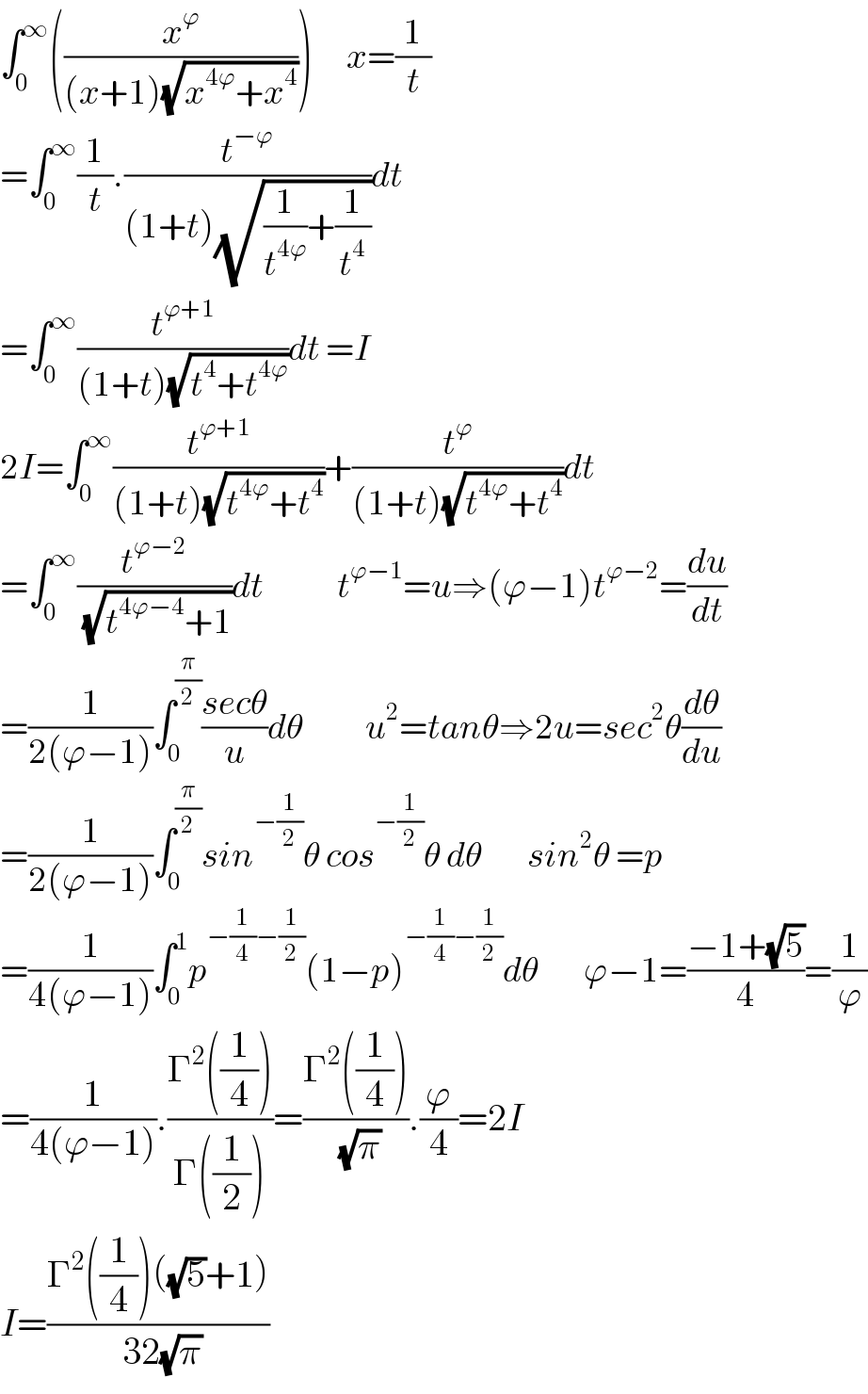
∫_0 ^∞ ((x^ϕ /((x+1)(√(x^(4ϕ) +x^4 ))))) x=(1/t) =∫_0 ^∞ (1/t).(t^(−ϕ) /((1+t)(√((1/t^(4ϕ) )+(1/t^4 )))))dt =∫_0 ^∞ (t^(ϕ+1) /((1+t)(√(t^4 +t^(4ϕ) ))))dt =I 2I=∫_0 ^∞ (t^(ϕ+1) /((1+t)(√(t^(4ϕ) +t^4 ))))+(t^ϕ /((1+t)(√(t^(4ϕ) +t^4 ))))dt =∫_0 ^∞ (t^(ϕ−2) /( (√(t^(4ϕ−4) +1))))dt t^(ϕ−1) =u⇒(ϕ−1)t^(ϕ−2) =(du/dt) =(1/(2(ϕ−1)))∫_0 ^(π/2) ((secθ)/u)dθ u^2 =tanθ⇒2u=sec^2 θ(dθ/du) =(1/(2(ϕ−1)))∫_0 ^(π/2) sin^(−(1/2)) θ cos^(−(1/2)) θ dθ sin^2 θ =p =(1/(4(ϕ−1)))∫_0 ^1 p^(−(1/4)−(1/2)) (1−p)^(−(1/4)−(1/2)) dθ ϕ−1=((−1+(√5))/4)=(1/ϕ) =(1/(4(ϕ−1))).((Γ^2 ((1/4)))/(Γ((1/2))))=((Γ^2 ((1/4)))/( (√π))).(ϕ/4)=2I I=((Γ^2 ((1/4))((√5)+1))/( 32(√π)))
$$\int_{\mathrm{0}} ^{\infty} \left(\frac{{x}^{\varphi} }{\left({x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{4}\varphi} +{x}^{\mathrm{4}} }}\right)\:\:\:\:\:\:{x}=\frac{\mathrm{1}}{{t}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{t}}.\frac{{t}^{−\varphi} }{\left(\mathrm{1}+{t}\right)\sqrt{\frac{\mathrm{1}}{{t}^{\mathrm{4}\varphi} }+\frac{\mathrm{1}}{{t}^{\mathrm{4}} }}}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\varphi+\mathrm{1}} }{\left(\mathrm{1}+{t}\right)\sqrt{{t}^{\mathrm{4}} +{t}^{\mathrm{4}\varphi} }}{dt}\:={I} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\varphi+\mathrm{1}} }{\left(\mathrm{1}+{t}\right)\sqrt{{t}^{\mathrm{4}\varphi} +{t}^{\mathrm{4}} }}+\frac{{t}^{\varphi} }{\left(\mathrm{1}+{t}\right)\sqrt{{t}^{\mathrm{4}\varphi} +{t}^{\mathrm{4}} }}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\varphi−\mathrm{2}} }{\:\sqrt{{t}^{\mathrm{4}\varphi−\mathrm{4}} +\mathrm{1}}}{dt}\:\:\:\:\:\:\:\:\:\:\:\:\:{t}^{\varphi−\mathrm{1}} ={u}\Rightarrow\left(\varphi−\mathrm{1}\right){t}^{\varphi−\mathrm{2}} =\frac{{du}}{{dt}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\left(\varphi−\mathrm{1}\right)}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sec}\theta}{{u}}{d}\theta\:\:\:\:\:\:\:\:\:\:\:{u}^{\mathrm{2}} ={tan}\theta\Rightarrow\mathrm{2}{u}={sec}^{\mathrm{2}} \theta\frac{{d}\theta}{{du}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\left(\varphi−\mathrm{1}\right)}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{−\frac{\mathrm{1}}{\mathrm{2}}} \theta\:{cos}^{−\frac{\mathrm{1}}{\mathrm{2}}} \theta\:{d}\theta\:\:\:\:\:\:\:\:{sin}^{\mathrm{2}} \theta\:={p} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\left(\varphi−\mathrm{1}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} {p}^{−\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−{p}\right)^{−\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}} {d}\theta\:\:\:\:\:\:\:\:\varphi−\mathrm{1}=\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}=\frac{\mathrm{1}}{\varphi} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\left(\varphi−\mathrm{1}\right)}.\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}=\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\:\sqrt{\pi}}.\frac{\varphi}{\mathrm{4}}=\mathrm{2}{I} \\ $$$${I}=\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)}{\:\mathrm{32}\sqrt{\pi}} \\ $$
Commented by mnjuly1970 last updated on 29/Nov/20
very nice solution bravo bravo sir payan .grateful...
$${very}\:{nice}\:{solution}\: \\ $$$${bravo}\:{bravo} \\ $$$${sir}\:\:{payan}\:.{grateful}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *