Menu Close

nice-calculus-prove-that-Apery-s-constant-0-1-4x-2-4-2-x-2-2-4-3-x-2-3-ln-2-x-x-1-x-dx-2-3-1-

Tinku Tara 0 Comments
Pin




Question Number 125098 by mnjuly1970 last updated on 08/Dec/20
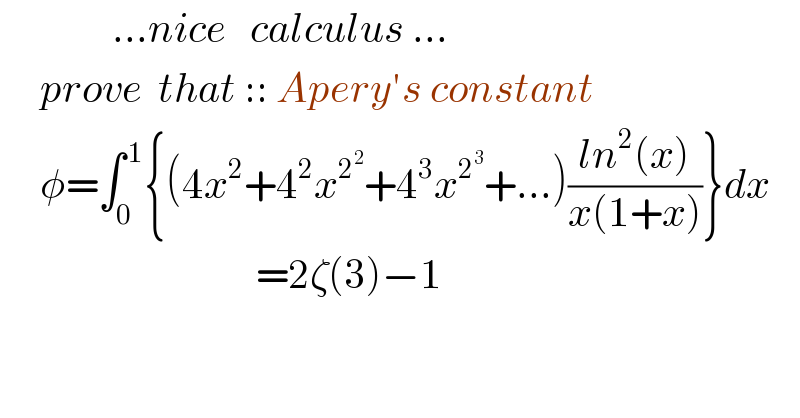
...nice calculus ... prove that :: Apery′s constant φ=∫_0 ^( 1) {(4x^2 +4^2 x^2^2 +4^3 x^2^3 +...)((ln^2 (x))/(x(1+x)))}dx =2ζ(3)−1
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:…{nice}\:\:\:{calculus}\:… \\ $$$$\:\:\:\:\:{prove}\:\:{that}\:::\:{Apery}'{s}\:{constant} \\ $$$$\:\:\:\:\:\phi=\int_{\mathrm{0}} ^{\:\mathrm{1}} \left\{\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} {x}^{\mathrm{2}^{\mathrm{2}} } +\mathrm{4}^{\mathrm{3}} {x}^{\mathrm{2}^{\mathrm{3}} } +…\right)\frac{{ln}^{\mathrm{2}} \left({x}\right)}{{x}\left(\mathrm{1}+{x}\right)}\right\}{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\zeta\left(\mathrm{3}\right)−\mathrm{1} \\ $$
Commented by talminator2856791 last updated on 08/Dec/20
what is the answer
$$\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{answer} \\ $$
Answered by Dwaipayan Shikari last updated on 08/Dec/20
∫_0 ^1 (4x^2 +4^2 x^2^2 +4^3 x^2^3 +..)((log^2 x)/(x(1+x)))dx =∫_0 ^1 Σ^∞ 4^n x^2^n ((log^2 x)/(x(1+x)))dx =Σ_(n=1) ^∞ ∫_0 ^1 ((2^(2n) x^2^n log^2 (x))/(x(1+x)))dx =Σ_(n≥1) ^∞ 2^(2n) (∫_0 ^1 x^(2^n −1) log^2 (x)−∫_0 ^1 ((x^2^n log^2 (x))/(1+x))dx) =Σ_(n≥1) ^∞ 2^(2n) (∫_(−∞) ^0 e^(2^n t) t^2 −∫_0 ^1 ((x^2^n log^2 (x))/(1+x))dx) Replace t as −t =Σ_(n≥1) ^∞ 2^(2n) (∫_0 ^∞ e^(−2^n t) t^2 −∫_0 ^1 ((x^2^n log^2 (x))/(1+x))dx) 2^n t=u⇒2^n =(du/dt) =Σ_(n≥1) ^∞ (1/2^n )Γ(2)−Σ_(n≥1) ^∞ 2^(2n) ∫_0 ^1 ((x^2^n log^2 (x))/(1+x))dx =1−Σ_(n≥1) ^∞ 2^(2n) Σ_(k≥0) ^∞ (−1)^k ∫_0 ^1 x^(2^n −k) log^2 (x)dx =1−Σ_(n≥1) ^∞ 2^(2n) Σ_(k≥0) ^∞ (−1)^k ∫_(−∞) ^0 e^(t(2^n −k+1)) t^2 dt =1−Σ_(n≥1) ^∞ 2^(2n) Σ_(k≥0) ^∞ (−1)^k ∫_0 ^∞ e^(−t(2^n −k+1)) t^2 dt =1−Σ_(n≥1) ^∞ 2^(2n) Σ_(k≥0) ^∞ (((−1)^k )/((2^n −k+1)^3 ))=1−Σ_(k≥0) ^∞ (−1)^k Σ_(n≥1) ^∞ (2^(2n) /((2^n −k+1)^3 ))...
$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} {x}^{\mathrm{2}^{\mathrm{2}} } +\mathrm{4}^{\mathrm{3}} {x}^{\mathrm{2}^{\mathrm{3}} } +..\right)\frac{{log}^{\mathrm{2}} {x}}{{x}\left(\mathrm{1}+{x}\right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \overset{\infty} {\sum}\mathrm{4}^{{n}} {x}^{\mathrm{2}^{{n}} } \frac{{log}^{\mathrm{2}} {x}}{{x}\left(\mathrm{1}+{x}\right)}{dx} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}^{\mathrm{2}{n}} {x}^{\mathrm{2}^{{n}} } {log}^{\mathrm{2}} \left({x}\right)}{{x}\left(\mathrm{1}+{x}\right)}{dx} \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{2}^{\mathrm{2}{n}} \left(\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}^{{n}} −\mathrm{1}} {log}^{\mathrm{2}} \left({x}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}^{{n}} } {log}^{\mathrm{2}} \left({x}\right)}{\mathrm{1}+{x}}{dx}\right) \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{2}^{\mathrm{2}{n}} \left(\int_{−\infty} ^{\mathrm{0}} {e}^{\mathrm{2}^{{n}} {t}} {t}^{\mathrm{2}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}^{{n}} } {log}^{\mathrm{2}} \left({x}\right)}{\mathrm{1}+{x}}{dx}\right)\:\:\:\:\:\:{Replace}\:{t}\:{as}\:−{t} \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{2}^{\mathrm{2}{n}} \left(\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}^{{n}} {t}} {t}^{\mathrm{2}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}^{{n}} } {log}^{\mathrm{2}} \left({x}\right)}{\mathrm{1}+{x}}{dx}\right)\:\:\:\:\:\:\:\:\:\mathrm{2}^{{n}} {t}={u}\Rightarrow\mathrm{2}^{{n}} =\frac{{du}}{{dt}} \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\Gamma\left(\mathrm{2}\right)−\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{2}^{\mathrm{2}{n}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}^{{n}} } {log}^{\mathrm{2}} \left({x}\right)}{\mathrm{1}+{x}}{dx} \\ $$$$=\mathrm{1}−\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{2}^{\mathrm{2}{n}} \underset{{k}\geqslant\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}^{{n}} −{k}} {log}^{\mathrm{2}} \left({x}\right){dx} \\ $$$$=\mathrm{1}−\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{2}^{\mathrm{2}{n}} \underset{{k}\geqslant\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}} \int_{−\infty} ^{\mathrm{0}} {e}^{{t}\left(\mathrm{2}^{{n}} −{k}+\mathrm{1}\right)} {t}^{\mathrm{2}} {dt} \\ $$$$=\mathrm{1}−\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{2}^{\mathrm{2}{n}} \underset{{k}\geqslant\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}} \int_{\mathrm{0}} ^{\infty} {e}^{−{t}\left(\mathrm{2}^{{n}} −{k}+\mathrm{1}\right)} {t}^{\mathrm{2}} {dt} \\ $$$$=\mathrm{1}−\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{2}^{\mathrm{2}{n}} \underset{{k}\geqslant\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{\left(\mathrm{2}^{{n}} −{k}+\mathrm{1}\right)^{\mathrm{3}} }=\mathrm{1}−\underset{{k}\geqslant\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}} \underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{\mathrm{2}{n}} }{\left(\mathrm{2}^{{n}} −{k}+\mathrm{1}\right)^{\mathrm{3}} }… \\ $$
Commented by talminator2856791 last updated on 08/Dec/20
is log the same as ln? because in the question it says ln but you say log
$$\:\mathrm{is}\:\mathrm{log}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{ln}?\: \\ $$$$\:\mathrm{because}\:\mathrm{in}\:\mathrm{the}\:\mathrm{question}\:\mathrm{it}\:\mathrm{says}\:\mathrm{ln}\:\mathrm{but}\:\mathrm{you}\:\mathrm{say}\:\mathrm{log} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *