nice-calculus-prove-that-i-pi-sinh-pi-Euler-gamma-function-m-n-july-1970-

Question Number 117979 by mnjuly1970 last updated on 14/Oct/20

\dots n i c e c a l c u l u s \dots

p r o v e t h a t :

∣ Γ (i) ∣ \overset{?}{=} \sqrt{\frac{π}{s i n h (π)}}

Γ : E u l e r g a m m a f u n c t i o n

\dots m . n . j u l y . 1970 \dots

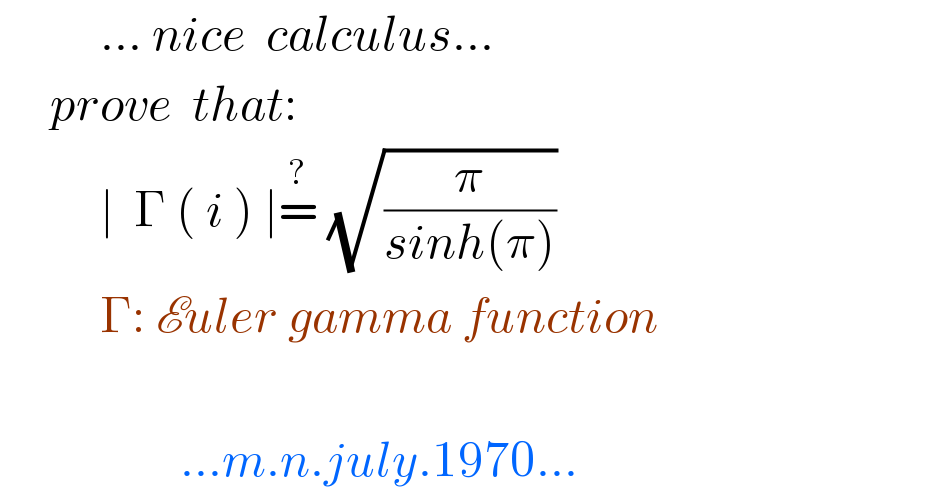
Commented by Lordose last updated on 14/Oct/20

THEY ARE NOT EQUAL

Answered by mindispower last updated on 14/Oct/20

Γ (1 - i) Γ (i) = \frac{π}{s i n (i π)}

Γ (1 - i) = - i Γ ((- i)

\Rightarrow Γ (- i) Γ (i) = \frac{π}{- i s i n (i π)} = \frac{π}{s h (π)}

Γ (- i) . Γ (i) = \frac{π}{s h (π)} \Rightarrow∣ Γ (i) ∣^{2} = \frac{π}{s h (π)}

∣ Γ (i) ∣= \sqrt{\frac{π}{s h (π)}}

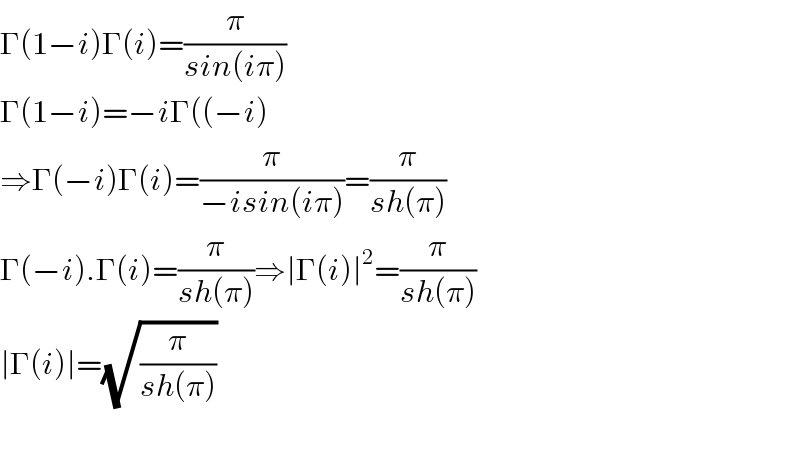
Commented by mnjuly1970 last updated on 14/Oct/20

t h a n k y o u

Commented by mindispower last updated on 14/Oct/20

w i t h e p l e a s u r