Question Number 120312 by mnjuly1970 last updated on 30/Oct/20
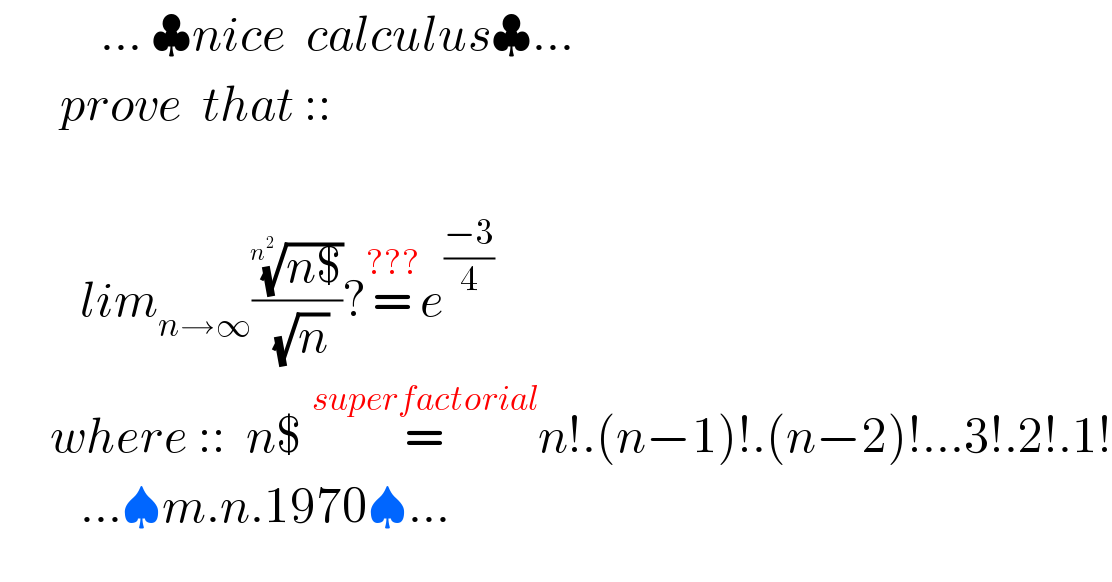
$$\:\:\:\:\:\:\:\:\:\:…\:\clubsuit{nice}\:\:{calculus}\clubsuit… \\ $$$$\:\:\:\:\:\:{prove}\:\:{that}\::: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:{lim}_{{n}\rightarrow\infty} \frac{\sqrt[{{n}^{\mathrm{2}} }]{{n\$}}}{\:\sqrt{{n}}}?\overset{???} {=}{e}^{\frac{−\mathrm{3}}{\mathrm{4}}} \\ $$$$\:\:\:\:\:{where}\:::\:\:{n\$}\:\overset{{superfactorial}} {=}{n}!.\left({n}−\mathrm{1}\right)!.\left({n}−\mathrm{2}\right)!…\mathrm{3}!.\mathrm{2}!.\mathrm{1}! \\ $$$$\:\:\:\:\:\:\:\:…\spadesuit{m}.{n}.\mathrm{1970}\spadesuit… \\ $$
Answered by mathmax by abdo last updated on 30/Oct/20
$$\mathrm{you}\:\mathrm{are}\:\mathrm{a}\:\mathrm{super}\:\mathrm{man}…. \\ $$
Commented by mnjuly1970 last updated on 31/Oct/20
$$\:{grateful}\:{sir}\:{max} \\ $$$$\:{thank}\:{you}\:{for}\:{your}\:{favor} \\ $$$${in}\:{fact}\:.{you}\:{are}\:{very}\:{very}\:{powerful}\:{and}\:{expert}\:{in}\:{mathematics}\:. \\ $$$${iam}\:{your}\:{student}\:{mr}\:{max}. \\ $$
Commented by mnjuly1970 last updated on 31/Oct/20

Commented by mathmax by abdo last updated on 01/Nov/20
$$\mathrm{you}\:\mathrm{are}\:\mathrm{always}\:\mathrm{welcome}..\mathrm{thanks} \\ $$
Commented by mnjuly1970 last updated on 01/Nov/20
$${sicerely}\:{yours} \\ $$$${m}.{n}.{july}.\mathrm{1970} \\ $$
