Menu Close

nice-calculus-prove-that-n-1-2n-1-1-n-1-ln-2-m-n-1970-

Tinku Tara 0 Comments
Pin




Question Number 122298 by mnjuly1970 last updated on 15/Nov/20
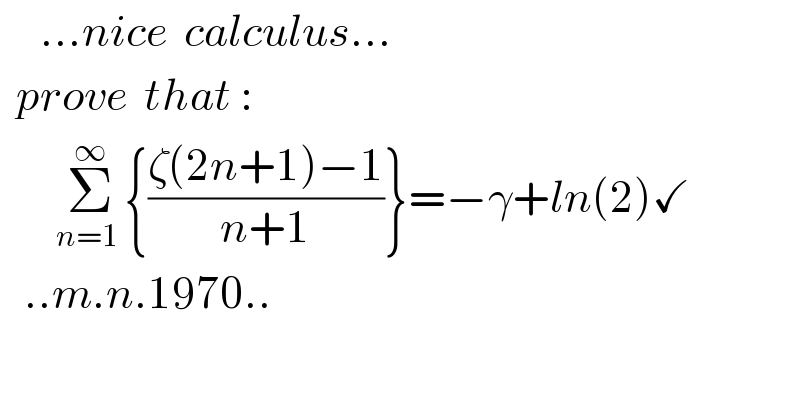
...nice calculus... prove that : Σ_(n=1 ) ^∞ {((ζ(2n+1)−1)/(n+1))}=−γ+ln(2)✓ ..m.n.1970..
$$\:\:\:\:\:…{nice}\:\:{calculus}… \\ $$$$\:\:{prove}\:\:{that}\::\:\: \\ $$$$\:\:\:\:\:\:\:\underset{{n}=\mathrm{1}\:} {\overset{\infty} {\sum}}\left\{\frac{\zeta\left(\mathrm{2}{n}+\mathrm{1}\right)−\mathrm{1}}{{n}+\mathrm{1}}\right\}=−\gamma+{ln}\left(\mathrm{2}\right)\checkmark \\ $$$$\:\:\:..{m}.{n}.\mathrm{1970}.. \\ $$
Answered by mindispower last updated on 17/Nov/20
ζ(s)−1=∫_0 ^∞ (x^(s−1) /(Γ(s)(e^x (e^x −1))))dx ⇒((ζ(2n+1)−1)/(n+1))=∫_0 ^∞ ((x^(2n) dx)/(Γ(2n+1)e^x (e^x −1))) Σ_(n≥1) ((ζ(2n+1)−1)/(n+1))=∫_0 ^∞ ((x^(2n) dx)/((n+1)Γ(2n+1)e^x (e^x −1)))..I Σ(x^(2n) /(2n!(n+1)))=(1/x^2 )Σ_(n≥1) (x^(2n+2) /(2n!(n+1)))=g(x) Σ_(n≥1) (x^(2n+2) /(2n!(n+1)))=f(x)⇒f′(x)=xΣ_(n≥1) ((2x^(2n) )/((2n!))) =2x(ch(x)−1) =2xsh(x)−2ch(x)−x^2 +2 f(x)=2xsh(x)−x^2 −2ch(x)+2 g(x)=((2sh(x))/(x ))−1−((2ch(x))/x^2 )+(2/(x^2 )) ∫_0 ^∞ ((2xsh(x)−x^2 −2ch(x)+2)/(x^2 e^x (e^x −1)))dx=S =∫_0 ^∞ ((xe^x −xe^(−x) −x^2 −e^x −e^(−x) +2)/(x^2 e^x (e^x −1)))dx =∫_0 ^∞ ((xe^(−x) −xe^(−3x) −x^2 e^(−2x) −e^(−x) −e^(−3x) +2e^(−2x) )/(x^2 (1−e^(−x) )))dx..E Ψ(z)=∫_0 ^∞ (e^(−t) /t)−(e^(−zt) /(1−e^(−t) ))dt ∫_0 ^∞ (e^(−t) /t)−(e^(−t) /(1−e^(−t) ))dt=Ψ(1) =∫_0 ^∞ ((e^(−t) −te^(−t) −e^(−2t) )/(t(1−e^(−t) )))dt..nice E=∫_0 ^∞ ((te^(−t) −t^2 e^(−t) −te^(−2t) +t^2 e^(−t) +te^(−2t) −te^(−3t) −t^2 e^(−2t) −e^(−t) −e^(−3t) +2e^(−2t) )/(t^2 (1−e^(−t) )))dt =Ψ(1)+∫_0 ^∞ ((t^2 e^(−t) (1−e^(−t) )+te^(−2t) (1−e^(−t) )−e^(−t) (1+e^(−2t) −2e^(−t) ))/(t^2 (1−e^(−t) )))dt =Ψ(1)+∫_0 ^∞ ((t^2 e^(−t) +te^(−2t) −e^(−t) (1−e^(−t) ))/t^2 )dt=Ψ(1)+T T=∫_0 ^∞ e^(−t) dt+∫_0 ^∞ ((te^(−2t) −e^(−t) +e^(−2t) )/t^2 )e^(−st) dt=1+w(s) T=w(0)+1 w′(s)=∫_0 ^∞ −e^(−(2+s)t) dt+∫_0 ^∞ ((e^(−t(1+s)) −e^(−t(2+s)) )/t) dt w′(s)=−(1/(2+s))−∫_0 ^∞ ∫_(2+s) ^(1+s) e^(−zt) dzdt w′(s)=−(1/(2+s))−∫_(2+s) ^(1+s) ∫_0 ^∞ e^(−zt) dtdz =−(1/(2+s))+ln(((2+s)/(1+s))) w(s)=−ln(2+s)+(s+2)ln(s+2)−(1+s)ln(1+s)+c w(s)=(s+1)ln(((s+2)/(s+1)))+c (s+1)ln(1+(1/(1+s)))+c lim_(s→∞) w(s)=0⇒lim_(s→∞) (s+1)ln(1+(1/(1+s)))+c=0 ⇒c=−1 ⇒w(0)=ln(1+1)−1=ln(2)−1 T=1+w(0)=ln(2) S=Ψ(1)+T=−γ+ln(2)...
$$\zeta\left({s}\right)−\mathrm{1}=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{s}−\mathrm{1}} }{\Gamma\left({s}\right)\left({e}^{{x}} \left({e}^{{x}} −\mathrm{1}\right)\right)}{dx} \\ $$$$\Rightarrow\frac{\zeta\left(\mathrm{2}{n}+\mathrm{1}\right)−\mathrm{1}}{{n}+\mathrm{1}}=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}{n}} {dx}}{\Gamma\left(\mathrm{2}{n}+\mathrm{1}\right){e}^{{x}} \left({e}^{{x}} −\mathrm{1}\right)} \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\zeta\left(\mathrm{2}{n}+\mathrm{1}\right)−\mathrm{1}}{{n}+\mathrm{1}}=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}{n}} {dx}}{\left({n}+\mathrm{1}\right)\Gamma\left(\mathrm{2}{n}+\mathrm{1}\right){e}^{{x}} \left({e}^{{x}} −\mathrm{1}\right)}..{I} \\ $$$$\Sigma\frac{{x}^{\mathrm{2}{n}} }{\mathrm{2}{n}!\left({n}+\mathrm{1}\right)}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{x}^{\mathrm{2}{n}+\mathrm{2}} }{\mathrm{2}{n}!\left({n}+\mathrm{1}\right)}={g}\left({x}\right) \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{x}^{\mathrm{2}{n}+\mathrm{2}} }{\mathrm{2}{n}!\left({n}+\mathrm{1}\right)}={f}\left({x}\right)\Rightarrow{f}'\left({x}\right)={x}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{2}{x}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}!\right)}\: \\ $$$$=\mathrm{2}{x}\left({ch}\left({x}\right)−\mathrm{1}\right) \\ $$$$=\mathrm{2}{xsh}\left({x}\right)−\mathrm{2}{ch}\left({x}\right)−{x}^{\mathrm{2}} +\mathrm{2} \\ $$$${f}\left({x}\right)=\mathrm{2}{xsh}\left({x}\right)−{x}^{\mathrm{2}} −\mathrm{2}{ch}\left({x}\right)+\mathrm{2} \\ $$$${g}\left({x}\right)=\frac{\mathrm{2}{sh}\left({x}\right)}{{x}\:}−\mathrm{1}−\frac{\mathrm{2}{ch}\left({x}\right)}{{x}^{\mathrm{2}} }+\frac{\mathrm{2}}{{x}^{\mathrm{2}} \:} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}{xsh}\left({x}\right)−{x}^{\mathrm{2}} −\mathrm{2}{ch}\left({x}\right)+\mathrm{2}}{{x}^{\mathrm{2}} {e}^{{x}} \left({e}^{{x}} −\mathrm{1}\right)}{dx}={S} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{xe}^{{x}} −{xe}^{−{x}} −{x}^{\mathrm{2}} −{e}^{{x}} −{e}^{−{x}} +\mathrm{2}}{{x}^{\mathrm{2}} {e}^{{x}} \left({e}^{{x}} −\mathrm{1}\right)}{dx} \\ $$$$ \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{xe}^{−{x}} −{xe}^{−\mathrm{3}{x}} −{x}^{\mathrm{2}} {e}^{−\mathrm{2}{x}} −{e}^{−{x}} −{e}^{−\mathrm{3}{x}} +\mathrm{2}{e}^{−\mathrm{2}{x}} }{{x}^{\mathrm{2}} \left(\mathrm{1}−{e}^{−{x}} \right)}{dx}..{E} \\ $$$$\Psi\left({z}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{t}} }{{t}}−\frac{{e}^{−{zt}} }{\mathrm{1}−{e}^{−{t}} }{dt} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{t}} }{{t}}−\frac{{e}^{−{t}} }{\mathrm{1}−{e}^{−{t}} }{dt}=\Psi\left(\mathrm{1}\right) \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{t}} −{te}^{−{t}} −{e}^{−\mathrm{2}{t}} }{{t}\left(\mathrm{1}−{e}^{−{t}} \right)}{dt}..{nice} \\ $$$${E}=\int_{\mathrm{0}} ^{\infty} \frac{{te}^{−{t}} −{t}^{\mathrm{2}} {e}^{−{t}} −{te}^{−\mathrm{2}{t}} +{t}^{\mathrm{2}} {e}^{−{t}} +{te}^{−\mathrm{2}{t}} −{te}^{−\mathrm{3}{t}} −{t}^{\mathrm{2}} {e}^{−\mathrm{2}{t}} −{e}^{−{t}} −{e}^{−\mathrm{3}{t}} +\mathrm{2}{e}^{−\mathrm{2}{t}} }{{t}^{\mathrm{2}} \left(\mathrm{1}−{e}^{−{t}} \right)}{dt} \\ $$$$=\Psi\left(\mathrm{1}\right)+\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\mathrm{2}} {e}^{−{t}} \left(\mathrm{1}−{e}^{−{t}} \right)+{te}^{−\mathrm{2}{t}} \left(\mathrm{1}−{e}^{−{t}} \right)−{e}^{−{t}} \left(\mathrm{1}+{e}^{−\mathrm{2}{t}} −\mathrm{2}{e}^{−{t}} \right)}{{t}^{\mathrm{2}} \left(\mathrm{1}−{e}^{−{t}} \right)}{dt} \\ $$$$=\Psi\left(\mathrm{1}\right)+\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\mathrm{2}} {e}^{−{t}} +{te}^{−\mathrm{2}{t}} −{e}^{−{t}} \left(\mathrm{1}−{e}^{−{t}} \right)}{{t}^{\mathrm{2}} }{dt}=\Psi\left(\mathrm{1}\right)+{T} \\ $$$${T}=\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} {dt}+\int_{\mathrm{0}} ^{\infty} \frac{{te}^{−\mathrm{2}{t}} −{e}^{−{t}} \:+{e}^{−\mathrm{2}{t}} }{{t}^{\mathrm{2}} }{e}^{−{st}} {dt}=\mathrm{1}+{w}\left({s}\right) \\ $$$${T}={w}\left(\mathrm{0}\right)+\mathrm{1} \\ $$$${w}'\left({s}\right)=\int_{\mathrm{0}} ^{\infty} −{e}^{−\left(\mathrm{2}+{s}\right){t}} {dt}+\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{t}\left(\mathrm{1}+{s}\right)} −{e}^{−{t}\left(\mathrm{2}+{s}\right)} }{{t}}\:{dt} \\ $$$${w}'\left({s}\right)=−\frac{\mathrm{1}}{\mathrm{2}+{s}}−\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{2}+{s}} ^{\mathrm{1}+{s}} {e}^{−{zt}} {dzdt} \\ $$$${w}'\left({s}\right)=−\frac{\mathrm{1}}{\mathrm{2}+{s}}−\int_{\mathrm{2}+{s}} ^{\mathrm{1}+{s}} \int_{\mathrm{0}} ^{\infty} {e}^{−{zt}} {dtdz} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}+{s}}+{ln}\left(\frac{\mathrm{2}+{s}}{\mathrm{1}+{s}}\right) \\ $$$${w}\left({s}\right)=−{ln}\left(\mathrm{2}+{s}\right)+\left({s}+\mathrm{2}\right){ln}\left({s}+\mathrm{2}\right)−\left(\mathrm{1}+{s}\right){ln}\left(\mathrm{1}+{s}\right)+{c} \\ $$$${w}\left({s}\right)=\left({s}+\mathrm{1}\right){ln}\left(\frac{{s}+\mathrm{2}}{{s}+\mathrm{1}}\right)+{c} \\ $$$$\left({s}+\mathrm{1}\right){ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+{s}}\right)+{c} \\ $$$$\underset{{s}\rightarrow\infty} {\mathrm{lim}}{w}\left({s}\right)=\mathrm{0}\Rightarrow\underset{{s}\rightarrow\infty} {\mathrm{lim}}\left({s}+\mathrm{1}\right){ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+{s}}\right)+{c}=\mathrm{0} \\ $$$$\Rightarrow{c}=−\mathrm{1} \\ $$$$\Rightarrow{w}\left(\mathrm{0}\right)={ln}\left(\mathrm{1}+\mathrm{1}\right)−\mathrm{1}={ln}\left(\mathrm{2}\right)−\mathrm{1} \\ $$$${T}=\mathrm{1}+{w}\left(\mathrm{0}\right)={ln}\left(\mathrm{2}\right) \\ $$$${S}=\Psi\left(\mathrm{1}\right)+{T}=−\gamma+{ln}\left(\mathrm{2}\right)… \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 18/Nov/20
bravo bravo sir mindspower . extraordinary my friend.(good)^∞
$${bravo}\:{bravo}\: \\ $$$${sir}\:{mindspower}\:. \\ $$$${extraordinary}\:{my}\:{friend}.\left({good}\right)^{\infty} \\ $$$$\:\:\:\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *