Question Number 124738 by mnjuly1970 last updated on 05/Dec/20
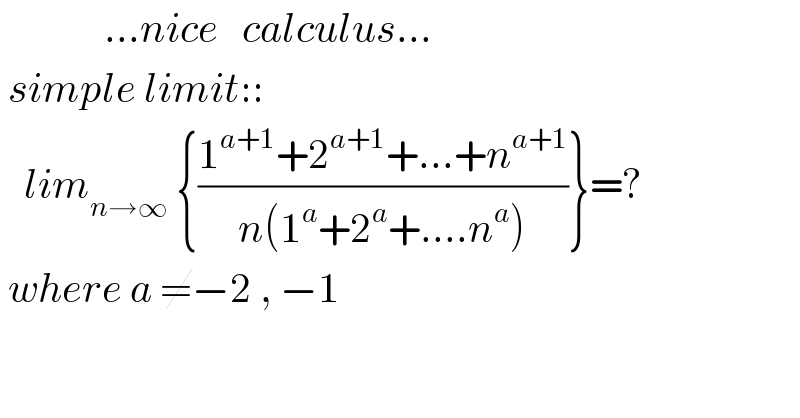
$$\:\:\:\:\:\:\:\:\:\:\:\:\:…{nice}\:\:\:{calculus}… \\ $$$$\:{simple}\:{limit}:: \\ $$$$\:\:\:{lim}_{{n}\rightarrow\infty} \:\left\{\frac{\mathrm{1}^{{a}+\mathrm{1}} +\mathrm{2}^{{a}+\mathrm{1}} +…+{n}^{{a}+\mathrm{1}} }{{n}\left(\mathrm{1}^{{a}} +\mathrm{2}^{{a}} +….{n}^{{a}} \right)}\right\}=? \\ $$$$\:{where}\:{a}\:\neq−\mathrm{2}\:,\:−\mathrm{1} \\ $$
Commented by PRITHWISH SEN 2 last updated on 07/Dec/20
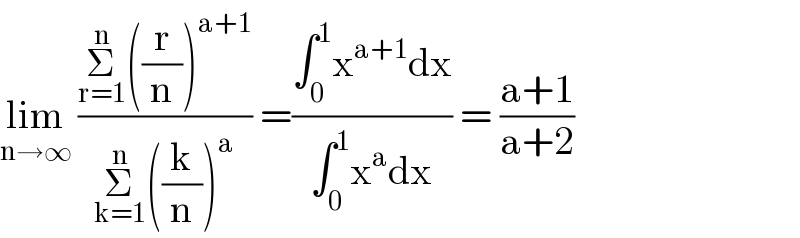
$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\underset{\mathrm{r}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\frac{\mathrm{r}}{\mathrm{n}}\right)^{\mathrm{a}+\mathrm{1}} }{\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\frac{\mathrm{k}}{\mathrm{n}}\right)^{\mathrm{a}} }\:=\frac{\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{a}+\mathrm{1}} \mathrm{dx}}{\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{a}} \mathrm{dx}}\:=\:\frac{\mathrm{a}+\mathrm{1}}{\mathrm{a}+\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 14/Dec/20

$${thank}\:{you}\:{sir}.. \\ $$
Commented by PRITHWISH SEN 2 last updated on 14/Dec/20

$$\mathrm{welcome} \\ $$
