Question Number 124587 by mnjuly1970 last updated on 04/Dec/20
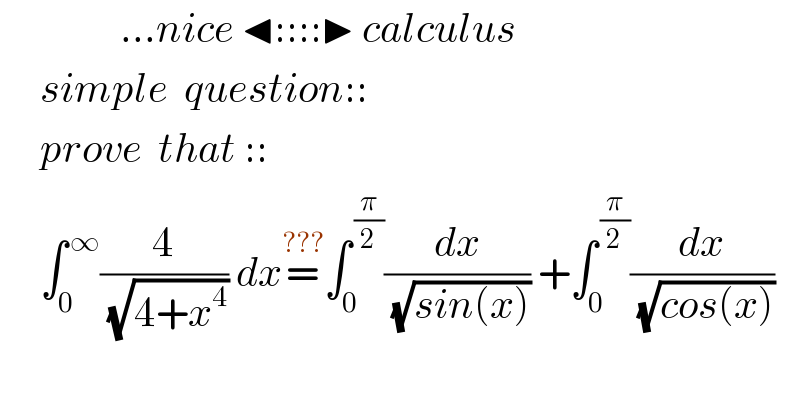
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…{nice}\:\blacktriangleleft::::\blacktriangleright\:{calculus} \\ $$$$\:\:\:\:\:{simple}\:\:{question}:: \\ $$$$\:\:\:\:\:{prove}\:\:{that}\::: \\ $$$$\:\:\:\:\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{4}}{\:\sqrt{\mathrm{4}+{x}^{\mathrm{4}} }}\:{dx}\overset{???} {=}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\:\sqrt{{sin}\left({x}\right)}}\:+\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\:\sqrt{{cos}\left({x}\right)}} \\ $$
Answered by mindispower last updated on 04/Dec/20
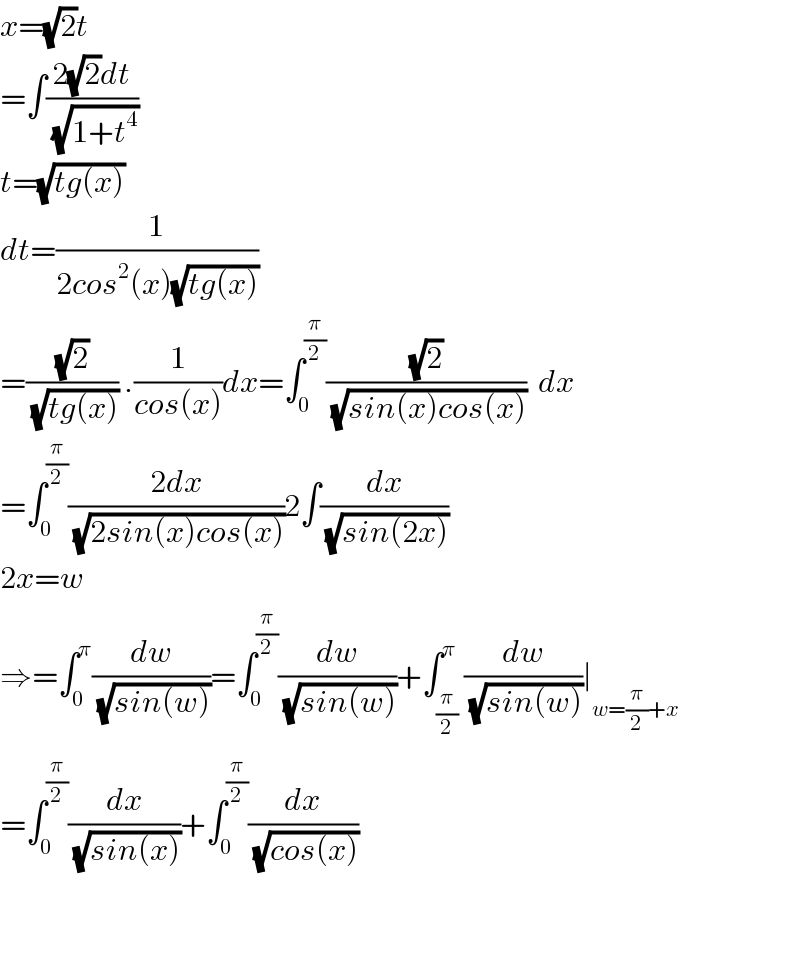
$${x}=\sqrt{\mathrm{2}}{t} \\ $$$$=\int\frac{\mathrm{2}\sqrt{\mathrm{2}}{dt}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{4}} }} \\ $$$${t}=\sqrt{{tg}\left({x}\right)} \\ $$$${dt}=\frac{\mathrm{1}}{\mathrm{2}{cos}^{\mathrm{2}} \left({x}\right)\sqrt{{tg}\left({x}\right)}} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{{tg}\left({x}\right)}}\:.\frac{\mathrm{1}}{{cos}\left({x}\right)}{dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\sqrt{\mathrm{2}}}{\:\sqrt{{sin}\left({x}\right){cos}\left({x}\right)}}\:\:{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2}{dx}}{\:\sqrt{\mathrm{2}{sin}\left({x}\right){cos}\left({x}\right)}}\mathrm{2}\int\frac{{dx}}{\:\sqrt{{sin}\left(\mathrm{2}{x}\right)}} \\ $$$$\mathrm{2}{x}={w} \\ $$$$\Rightarrow=\int_{\mathrm{0}} ^{\pi} \frac{{dw}}{\:\sqrt{{sin}\left({w}\right)}}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dw}}{\:\sqrt{{sin}\left({w}\right)}}+\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \frac{{dw}}{\:\sqrt{{sin}\left({w}\right)}}\mid_{{w}=\frac{\pi}{\mathrm{2}}+{x}} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\:\sqrt{{sin}\left({x}\right)}}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\:\sqrt{{cos}\left({x}\right)}} \\ $$$$ \\ $$$$ \\ $$
Commented by mindispower last updated on 05/Dec/20

$${withe}\:{plesur} \\ $$
Commented by mnjuly1970 last updated on 04/Dec/20
$${excellent}.{sir}\:{mindspower} \\ $$$${as}\:{always}… \\ $$
