Question Number 125096 by mnjuly1970 last updated on 08/Dec/20
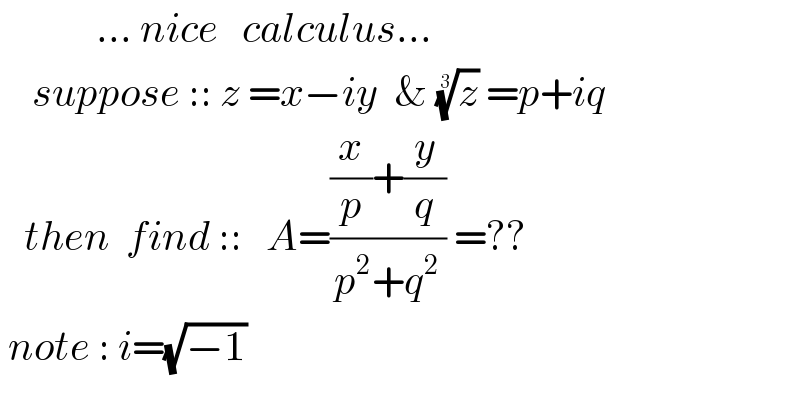
$$\:\:\:\:\:\:\:\:\:\:\:\:…\:{nice}\:\:\:{calculus}… \\ $$$$\:\:\:\:{suppose}\:::\:{z}\:={x}−{iy}\:\:\&\:\sqrt[{\mathrm{3}}]{{z}}\:={p}+{iq} \\ $$$$\:\:\:{then}\:\:{find}\:::\:\:\:{A}=\frac{\frac{{x}}{{p}}+\frac{{y}}{{q}}}{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }\:=?? \\ $$$$\:{note}\::\:{i}=\sqrt{−\mathrm{1}} \\ $$
Answered by MJS_new last updated on 08/Dec/20
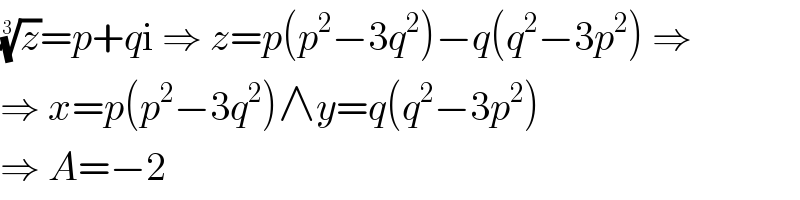
$$\sqrt[{\mathrm{3}}]{{z}}={p}+{q}\mathrm{i}\:\Rightarrow\:{z}={p}\left({p}^{\mathrm{2}} −\mathrm{3}{q}^{\mathrm{2}} \right)−{q}\left({q}^{\mathrm{2}} −\mathrm{3}{p}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$$\Rightarrow\:{x}={p}\left({p}^{\mathrm{2}} −\mathrm{3}{q}^{\mathrm{2}} \right)\wedge{y}={q}\left({q}^{\mathrm{2}} −\mathrm{3}{p}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:{A}=−\mathrm{2} \\ $$
Commented by mnjuly1970 last updated on 08/Dec/20
$$\:{thanks}\:{alot}\:{sir}\:{MJS}.{grateful}.. \\ $$
