Menu Close

nice-cslculus-find-L-te-t-ln-t-transform-laplace-

Tinku Tara 0 Comments
Pin




Question Number 130200 by mnjuly1970 last updated on 23/Jan/21
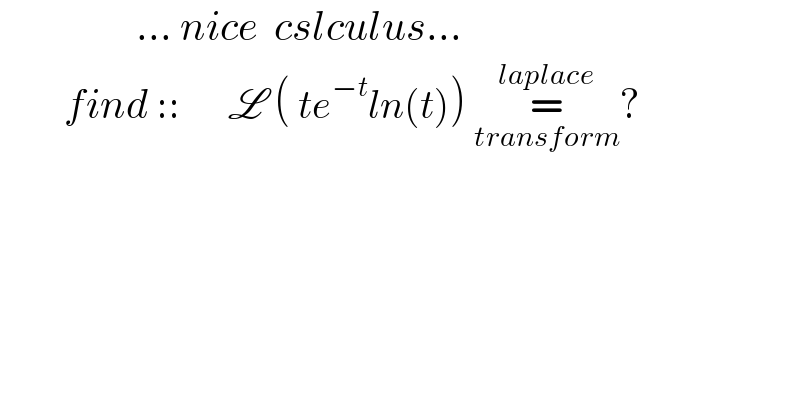
... nice cslculus... find :: L ( te^(−t) ln(t)) =_(transform) ^(laplace) ?
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\:{nice}\:\:{cslculus}… \\ $$$$\:\:\:\:\:\:\:\:{find}\:::\:\:\:\:\:\:\mathscr{L}\:\left(\:{te}^{−{t}} {ln}\left({t}\right)\right)\:\underset{{transform}} {\overset{{laplace}} {=}}? \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$
Answered by Dwaipayan Shikari last updated on 23/Jan/21
∫_0 ^∞ e^(−(s+1)t) tlog(t)dt (s+1)u =(1/((s+1)^2 ))∫_0 ^∞ e^(−u) ulog(u)−((log(s+1))/((s+1)^2 ))∫_0 ^∞ ue^(−u) =((ψ(2)−log(1+s))/((s+1)^2 ))=−((γ+1+log(1+s))/((s+1)^2 ))
$$\int_{\mathrm{0}} ^{\infty} {e}^{−\left({s}+\mathrm{1}\right){t}} {tlog}\left({t}\right){dt}\:\:\:\:\:\:\:\:\left({s}+\mathrm{1}\right){u} \\ $$$$=\frac{\mathrm{1}}{\left({s}+\mathrm{1}\right)^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} {e}^{−{u}} {ulog}\left({u}\right)−\frac{{log}\left({s}+\mathrm{1}\right)}{\left({s}+\mathrm{1}\right)^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} {ue}^{−{u}} \\ $$$$=\frac{\psi\left(\mathrm{2}\right)−{log}\left(\mathrm{1}+{s}\right)}{\left({s}+\mathrm{1}\right)^{\mathrm{2}} }=−\frac{\gamma+\mathrm{1}+{log}\left(\mathrm{1}+{s}\right)}{\left({s}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Commented by mnjuly1970 last updated on 23/Jan/21
thank you mercey...
$${thank}\:{you}\: \\ $$$${mercey}… \\ $$
Answered by mathmax by abdo last updated on 23/Jan/21
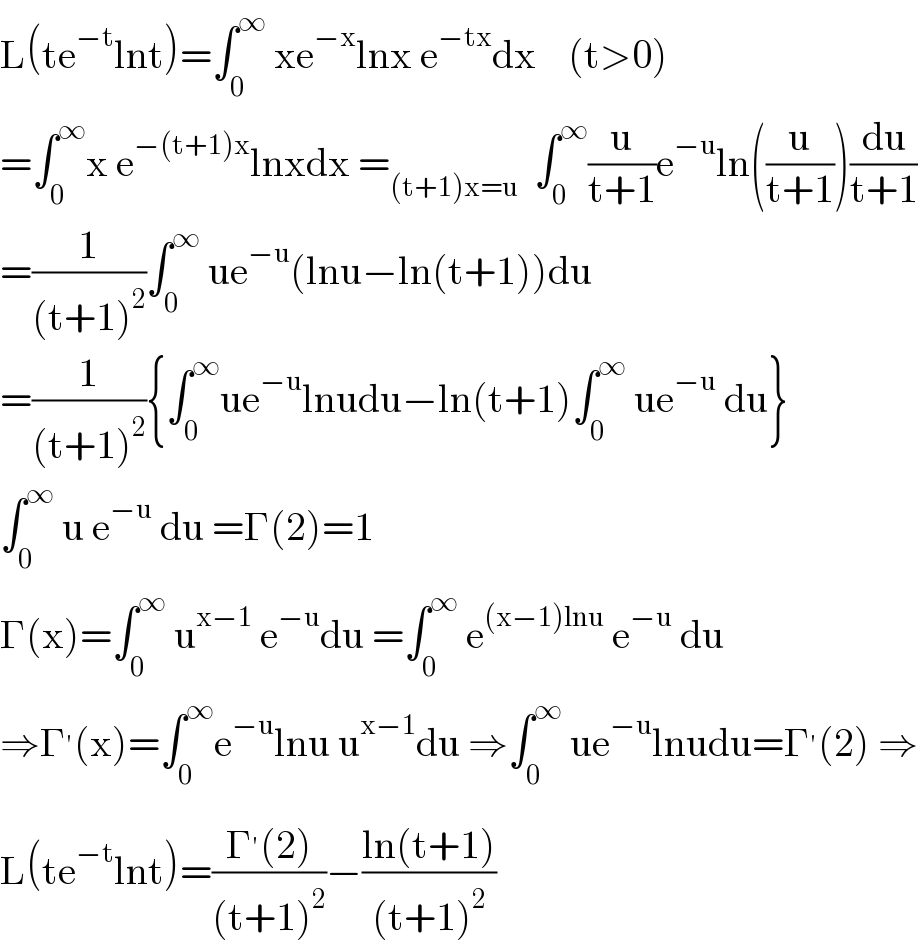
L(te^(−t) lnt)=∫_0 ^∞ xe^(−x) lnx e^(−tx) dx (t>0) =∫_0 ^∞ x e^(−(t+1)x) lnxdx =_((t+1)x=u) ∫_0 ^∞ (u/(t+1))e^(−u) ln((u/(t+1)))(du/(t+1)) =(1/((t+1)^2 ))∫_0 ^∞ ue^(−u) (lnu−ln(t+1))du =(1/((t+1)^2 )){∫_0 ^∞ ue^(−u) lnudu−ln(t+1)∫_0 ^∞ ue^(−u) du} ∫_0 ^∞ u e^(−u) du =Γ(2)=1 Γ(x)=∫_0 ^∞ u^(x−1) e^(−u) du =∫_0 ^∞ e^((x−1)lnu) e^(−u) du ⇒Γ^′ (x)=∫_0 ^∞ e^(−u) lnu u^(x−1) du ⇒∫_0 ^∞ ue^(−u) lnudu=Γ^′ (2) ⇒ L(te^(−t) lnt)=((Γ^′ (2))/((t+1)^2 ))−((ln(t+1))/((t+1)^2 ))
$$\mathrm{L}\left(\mathrm{te}^{−\mathrm{t}} \mathrm{lnt}\right)=\int_{\mathrm{0}} ^{\infty} \:\mathrm{xe}^{−\mathrm{x}} \mathrm{lnx}\:\mathrm{e}^{−\mathrm{tx}} \mathrm{dx}\:\:\:\:\left(\mathrm{t}>\mathrm{0}\right) \\ $$$$=\int_{\mathrm{0}} ^{\infty} \mathrm{x}\:\mathrm{e}^{−\left(\mathrm{t}+\mathrm{1}\right)\mathrm{x}} \mathrm{lnxdx}\:=_{\left(\mathrm{t}+\mathrm{1}\right)\mathrm{x}=\mathrm{u}} \:\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{u}}{\mathrm{t}+\mathrm{1}}\mathrm{e}^{−\mathrm{u}} \mathrm{ln}\left(\frac{\mathrm{u}}{\mathrm{t}+\mathrm{1}}\right)\frac{\mathrm{du}}{\mathrm{t}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \:\mathrm{ue}^{−\mathrm{u}} \left(\mathrm{lnu}−\mathrm{ln}\left(\mathrm{t}+\mathrm{1}\right)\right)\mathrm{du} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} }\left\{\int_{\mathrm{0}} ^{\infty} \mathrm{ue}^{−\mathrm{u}} \mathrm{lnudu}−\mathrm{ln}\left(\mathrm{t}+\mathrm{1}\right)\int_{\mathrm{0}} ^{\infty} \:\mathrm{ue}^{−\mathrm{u}} \:\mathrm{du}\right\} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{u}\:\mathrm{e}^{−\mathrm{u}} \:\mathrm{du}\:=\Gamma\left(\mathrm{2}\right)=\mathrm{1} \\ $$$$\Gamma\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\infty} \:\mathrm{u}^{\mathrm{x}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{u}} \mathrm{du}\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\left(\mathrm{x}−\mathrm{1}\right)\mathrm{lnu}} \:\mathrm{e}^{−\mathrm{u}} \:\mathrm{du} \\ $$$$\Rightarrow\Gamma^{'} \left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{u}} \mathrm{lnu}\:\mathrm{u}^{\mathrm{x}−\mathrm{1}} \mathrm{du}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\mathrm{ue}^{−\mathrm{u}} \mathrm{lnudu}=\Gamma^{'} \left(\mathrm{2}\right)\:\Rightarrow \\ $$$$\mathrm{L}\left(\mathrm{te}^{−\mathrm{t}} \mathrm{lnt}\right)=\frac{\Gamma^{'} \left(\mathrm{2}\right)}{\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{ln}\left(\mathrm{t}+\mathrm{1}\right)}{\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *