Question Number 165255 by amin96 last updated on 28/Jan/22
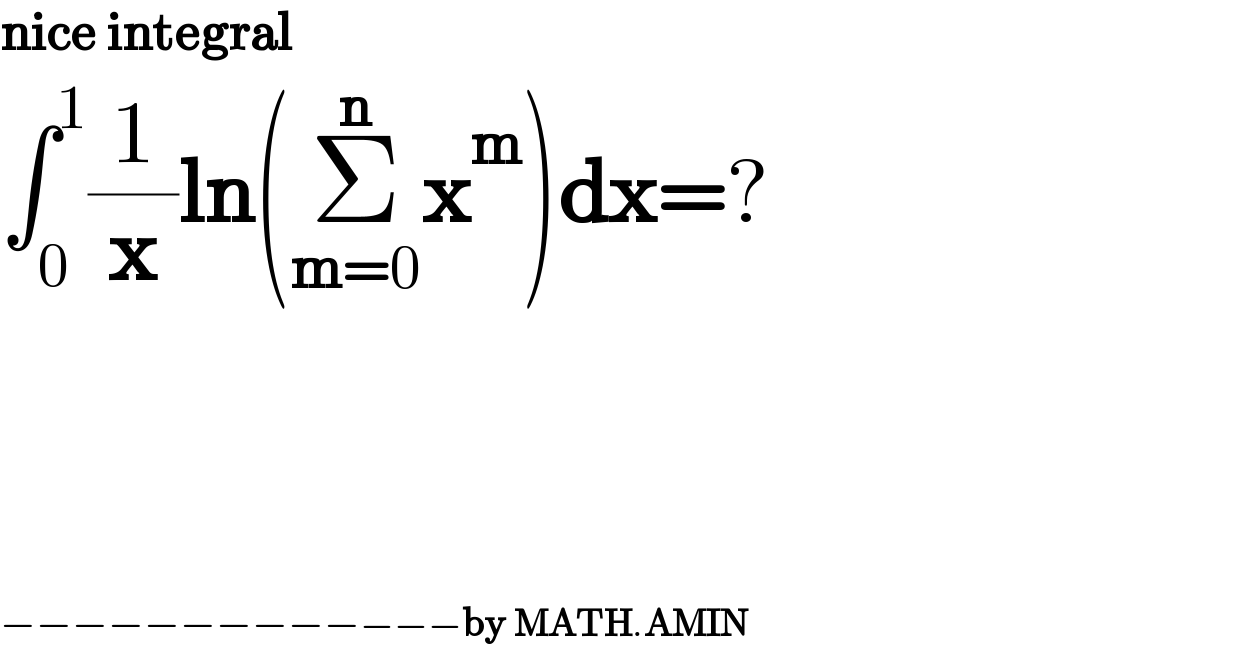
$$\boldsymbol{\mathrm{nice}}\:\boldsymbol{\mathrm{integral}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}\boldsymbol{\mathrm{ln}}\left(\underset{\boldsymbol{\mathrm{m}}=\mathrm{0}} {\overset{\boldsymbol{\mathrm{n}}} {\sum}}\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{m}}} \right)\boldsymbol{\mathrm{dx}}=? \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$−−−−−−−−−−−−−\boldsymbol{\mathrm{by}}\:\boldsymbol{\mathrm{MATH}}.\boldsymbol{\mathrm{AMIN}} \\ $$
Answered by mindispower last updated on 28/Jan/22
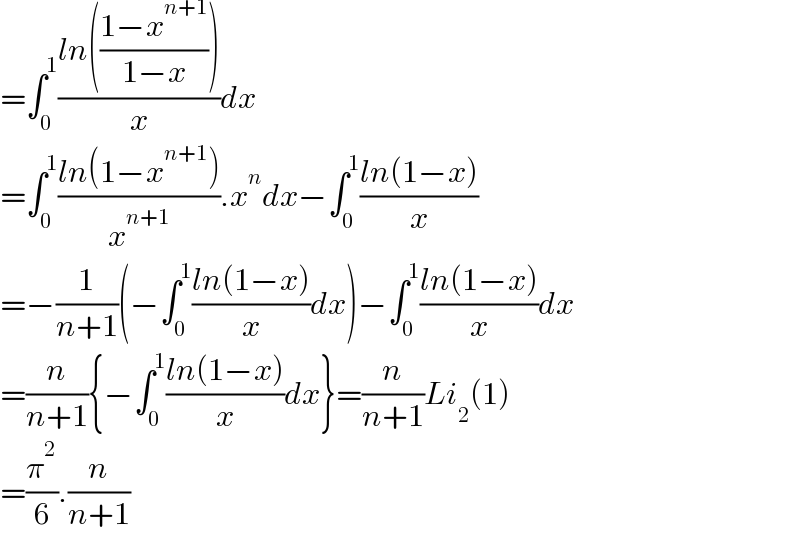
$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\frac{\mathrm{1}−{x}^{{n}+\mathrm{1}} }{\mathrm{1}−{x}}\right)}{{x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}^{{n}+\mathrm{1}} \right)}{{x}^{{n}+\mathrm{1}} }.{x}^{{n}} {dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}\right)}{{x}} \\ $$$$=−\frac{\mathrm{1}}{{n}+\mathrm{1}}\left(−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}\right)}{{x}}{dx}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}\right)}{{x}}{dx} \\ $$$$=\frac{{n}}{{n}+\mathrm{1}}\left\{−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}\right)}{{x}}{dx}\right\}=\frac{{n}}{{n}+\mathrm{1}}{Li}_{\mathrm{2}} \left(\mathrm{1}\right) \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}.\frac{{n}}{{n}+\mathrm{1}} \\ $$
Commented by amin96 last updated on 28/Jan/22
$$\boldsymbol{\mathrm{nice}}\:\boldsymbol{\mathrm{solution}}\:\boldsymbol{\mathrm{sir}}.\:\boldsymbol{\mathrm{greatefull}} \\ $$
Commented by mindispower last updated on 28/Jan/22
$${Withe}\:{Pleasur}\:{Have}\:{a}\:{nice}\:{Day} \\ $$
