Question Number 129936 by liberty last updated on 21/Jan/21
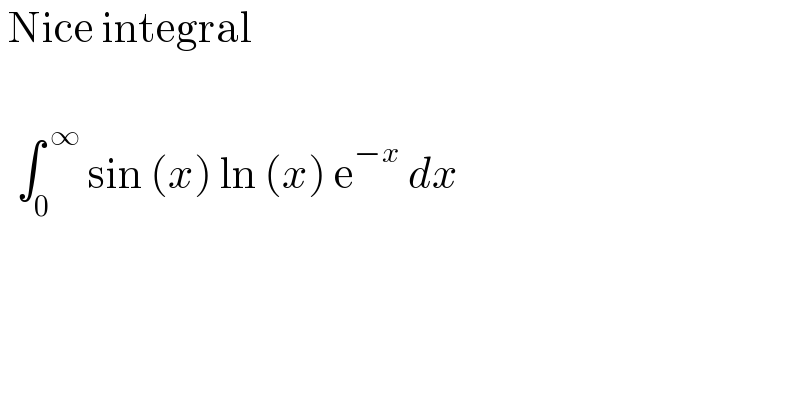
$$\:\mathrm{Nice}\:\mathrm{integral}\: \\ $$$$ \\ $$$$\:\:\int_{\mathrm{0}} ^{\:\infty} \:\mathrm{sin}\:\left({x}\right)\:\mathrm{ln}\:\left({x}\right)\:\mathrm{e}^{−{x}} \:{dx}\: \\ $$
Answered by Lordose last updated on 21/Jan/21
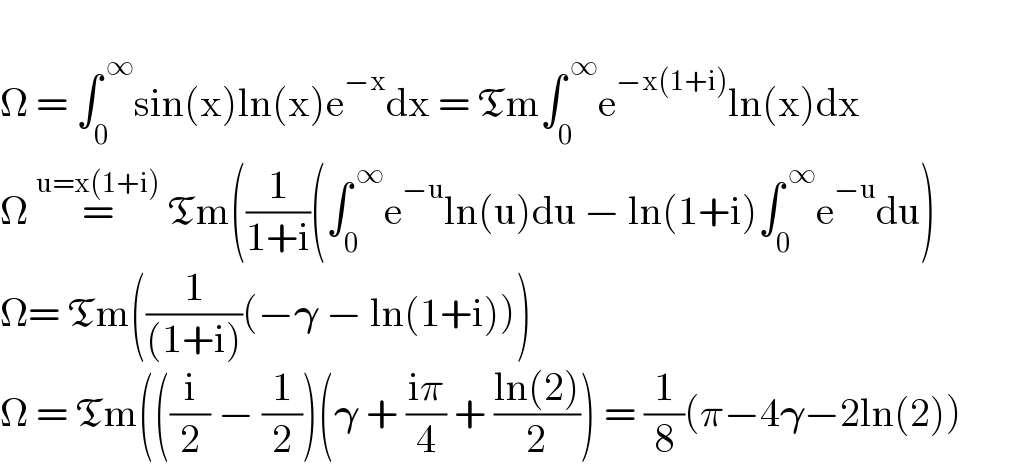
$$ \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\infty} \mathrm{sin}\left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{x}\right)\mathrm{e}^{−\mathrm{x}} \mathrm{dx}\:=\:\mathfrak{T}\mathrm{m}\int_{\mathrm{0}} ^{\:\infty} \mathrm{e}^{−\mathrm{x}\left(\mathrm{1}+\mathrm{i}\right)} \mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\Omega\:\overset{\mathrm{u}=\mathrm{x}\left(\mathrm{1}+\mathrm{i}\right)} {=}\:\mathfrak{T}\mathrm{m}\left(\frac{\mathrm{1}}{\mathrm{1}+\mathrm{i}}\left(\int_{\mathrm{0}} ^{\:\infty} \mathrm{e}^{−\mathrm{u}} \mathrm{ln}\left(\mathrm{u}\right)\mathrm{du}\:−\:\mathrm{ln}\left(\mathrm{1}+\mathrm{i}\right)\int_{\mathrm{0}} ^{\:\infty} \mathrm{e}^{−\mathrm{u}} \mathrm{du}\right)\right. \\ $$$$\Omega=\:\mathfrak{T}\mathrm{m}\left(\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{i}\right)}\left(−\boldsymbol{\gamma}\:−\:\mathrm{ln}\left(\mathrm{1}+\mathrm{i}\right)\right)\right) \\ $$$$\Omega\:=\:\mathfrak{T}\mathrm{m}\left(\left(\frac{\mathrm{i}}{\mathrm{2}}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\boldsymbol{\gamma}\:+\:\frac{\mathrm{i}\pi}{\mathrm{4}}\:+\:\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{8}}\left(\pi−\mathrm{4}\boldsymbol{\gamma}−\mathrm{2ln}\left(\mathrm{2}\right)\right)\:\:\:\:\:\:\:\:\:\right. \\ $$
Commented by mnjuly1970 last updated on 21/Jan/21
$${nice}\:\:{very}\:\:{nice}… \\ $$
Answered by bemath last updated on 21/Jan/21
![B=∫_0 ^( ∞) sin (x)ln (x)e^(−x) dx by Frullani integral ln (x)=∫_0 ^( ∞) ((e^(−y) −e^(−xy) )/y) dy now I=∫_(0 ) ^∞ e^(−x) sin (x)∫_0 ^( ∞) ((e^(−y) −e^(−xy) )/y) dy dx = ∫_0 ^( ∞) ∫_0 ^∞ (((e^(−(x+y)) −e^(−x(y+1)) )/y))sin (x) dy dx = ∫_0 ^∞ (1/y) ∫_0 ^∞ (e^(−(x+y)) −e^(−x(y+1)) ) dx dy = ∫_0 ^∞ (1/y)((1/2)e^(−y) −(1/((y+1)^2 +1))) dy first term ∫_ε ^∞ (1/(2y))e^(−y) dy = (1/2)e^(−y) ln y ∣_ε ^∞ −∫_ε ^∞ −(1/2)e^(−y) ln y dy = −(1/2)e^(−ε) ln ε +(1/2)∫_ε ^∞ e^(−y) ln y dy second term ∫_ε ^∞ (1/(y((y+1)^2 +1)))dy = (1/2)∫_ε ^∞ ((1/y)−(((y+1)+1)/((y+1)^2 +1)))dy = (1/2)(ln y−(1/2)ln ((y+1)^2 +1)−arctan (y+1))∣_ε ^∞ = (1/4)[ ln ((y^2 /((y+1)^2 +1)))−2arctan (y+1)]_ε ^∞ = (1/4) [−ln ((ε^2 /((1+ε)^2 +1)))−π + 2arctan (ε+1) ] letting ε→0^+ and nothing that ∫_0 ^∞ e^(−y) ln y dy=−γ thus we get B=−(1/2)γ−(1/4)ln (2)+(π/8)](https://www.tinkutara.com/question/Q129945.png)
$$\:\mathrm{B}=\int_{\mathrm{0}} ^{\:\infty} \mathrm{sin}\:\left(\mathrm{x}\right)\mathrm{ln}\:\left(\mathrm{x}\right)\mathrm{e}^{−\mathrm{x}} \:\mathrm{dx}\: \\ $$$$\mathrm{by}\:\mathrm{Frullani}\:\mathrm{integral}\:\mathrm{ln}\:\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\:\infty} \:\frac{\mathrm{e}^{−\mathrm{y}} −\mathrm{e}^{−\mathrm{xy}} }{\mathrm{y}}\:\mathrm{dy} \\ $$$$\mathrm{now}\:\mathrm{I}=\int_{\mathrm{0}\:} ^{\infty} \mathrm{e}^{−\mathrm{x}} \mathrm{sin}\:\left(\mathrm{x}\right)\int_{\mathrm{0}} ^{\:\infty} \:\frac{\mathrm{e}^{−\mathrm{y}} −\mathrm{e}^{−\mathrm{xy}} }{\mathrm{y}}\:\mathrm{dy}\:\mathrm{dx} \\ $$$$\:=\:\int_{\mathrm{0}} ^{\:\infty} \int_{\mathrm{0}} ^{\infty} \:\left(\frac{\mathrm{e}^{−\left(\mathrm{x}+\mathrm{y}\right)} −\mathrm{e}^{−\mathrm{x}\left(\mathrm{y}+\mathrm{1}\right)} }{\mathrm{y}}\right)\mathrm{sin}\:\left(\mathrm{x}\right)\:\mathrm{dy}\:\mathrm{dx} \\ $$$$\:=\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{y}}\:\int_{\mathrm{0}} ^{\infty} \:\left(\mathrm{e}^{−\left(\mathrm{x}+\mathrm{y}\right)} −\mathrm{e}^{−\mathrm{x}\left(\mathrm{y}+\mathrm{1}\right)} \right)\:\mathrm{dx}\:\mathrm{dy}\: \\ $$$$\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{y}}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{y}} −\frac{\mathrm{1}}{\left(\mathrm{y}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}\right)\:\mathrm{dy} \\ $$$$\:\mathrm{first}\:\mathrm{term}\:\int_{\epsilon} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{2y}}\mathrm{e}^{−\mathrm{y}} \:\mathrm{dy}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{y}} \mathrm{ln}\:\mathrm{y}\:\mid_{\epsilon} ^{\infty} −\int_{\epsilon} ^{\infty} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{y}} \mathrm{ln}\:\mathrm{y}\:\mathrm{dy} \\ $$$$\:\:\:\:\:\:\:\:\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\epsilon} \:\mathrm{ln}\:\epsilon\:+\frac{\mathrm{1}}{\mathrm{2}}\int_{\epsilon} ^{\infty} \:\mathrm{e}^{−\mathrm{y}} \mathrm{ln}\:\mathrm{y}\:\mathrm{dy} \\ $$$$\mathrm{second}\:\mathrm{term}\:\int_{\epsilon} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{y}\left(\left(\mathrm{y}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\right)}\mathrm{dy}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\epsilon} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{y}}−\frac{\left(\mathrm{y}+\mathrm{1}\right)+\mathrm{1}}{\left(\mathrm{y}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}\right)\mathrm{dy} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{ln}\:\mathrm{y}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\left(\mathrm{y}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{arctan}\:\left(\mathrm{y}+\mathrm{1}\right)\right)\mid_{\epsilon} ^{\infty} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}\left[\:\mathrm{ln}\:\left(\frac{\mathrm{y}^{\mathrm{2}} }{\left(\mathrm{y}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}\right)−\mathrm{2arctan}\:\left(\mathrm{y}+\mathrm{1}\right)\right]_{\epsilon} ^{\infty} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:\left[−\mathrm{ln}\:\left(\frac{\epsilon^{\mathrm{2}} }{\left(\mathrm{1}+\epsilon\right)^{\mathrm{2}} +\mathrm{1}}\right)−\pi\:+\:\mathrm{2arctan}\:\left(\epsilon+\mathrm{1}\right)\:\right] \\ $$$$\mathrm{letting}\:\epsilon\rightarrow\mathrm{0}^{+} \:\mathrm{and}\:\mathrm{nothing}\:\mathrm{that}\:\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{y}} \mathrm{ln}\:\mathrm{y}\:\mathrm{dy}=−\gamma \\ $$$$\mathrm{thus}\:\mathrm{we}\:\mathrm{get}\:\mathrm{B}=−\frac{\mathrm{1}}{\mathrm{2}}\gamma−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left(\mathrm{2}\right)+\frac{\pi}{\mathrm{8}} \\ $$$$ \\ $$
