nice-integral-please-evaluate-I-0-1-sin-x-sin-1-x-dx-x-m-n-1970-

Question Number 117948 by mnjuly1970 last updated on 14/Oct/20

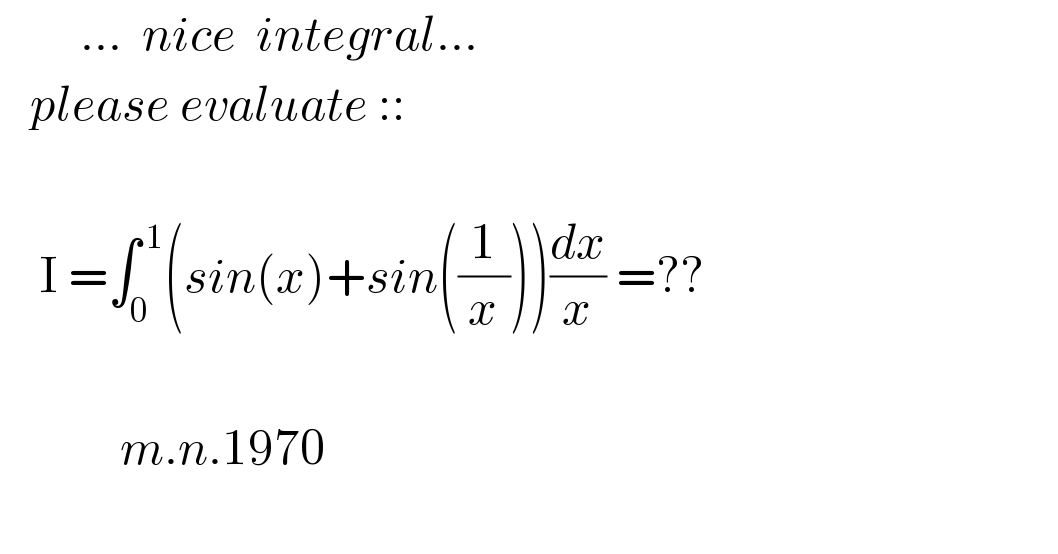
$$\:\:\:\:\:\:\:\:…\:\:{nice}\:\:{integral}…\: \\ $$$$\:\:\:{please}\:{evaluate}\::: \\ $$$$ \\ $$$$\:\:\:\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\:\mathrm{1}} \left({sin}\left({x}\right)+{sin}\left(\frac{\mathrm{1}}{{x}}\right)\right)\frac{{dx}}{{x}}\:=?? \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{m}.{n}.\mathrm{1970} \\ $$$$\:\: \\ $$

Answered by Lordose last updated on 14/Oct/20

I=∫_( 0) ^( 1) ((sinx)/x)dx + ∫_( 0) ^( 1) ((sin((1/x)))/x)dx I= ∣Si(x)∣_0 ^1 −∣Si((1/x))∣_0 ^1 I= Si(1)−Si(0) − Si(1) + Si(∞) I= (π/2)

$$ \\ $$$$\mathrm{I}=\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{sinx}}{\mathrm{x}}\mathrm{dx}\:+\:\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{sin}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$\mathrm{I}=\:\mid\mathrm{Si}\left(\mathrm{x}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \:−\mid\mathrm{Si}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\mathrm{I}=\:\mathrm{Si}\left(\mathrm{1}\right)−\mathrm{Si}\left(\mathrm{0}\right)\:−\:\mathrm{Si}\left(\mathrm{1}\right)\:+\:\mathrm{Si}\left(\infty\right) \\ $$$$\mathrm{I}=\:\frac{\pi}{\mathrm{2}} \\ $$

Commented by mnjuly1970 last updated on 14/Oct/20

$${grateful}.. \\ $$

Answered by AbduraufKodiriy last updated on 14/Oct/20

Commented by mnjuly1970 last updated on 14/Oct/20

$${thank}\:{you}\:.. \\ $$

Answered by 1549442205PVT last updated on 14/Oct/20

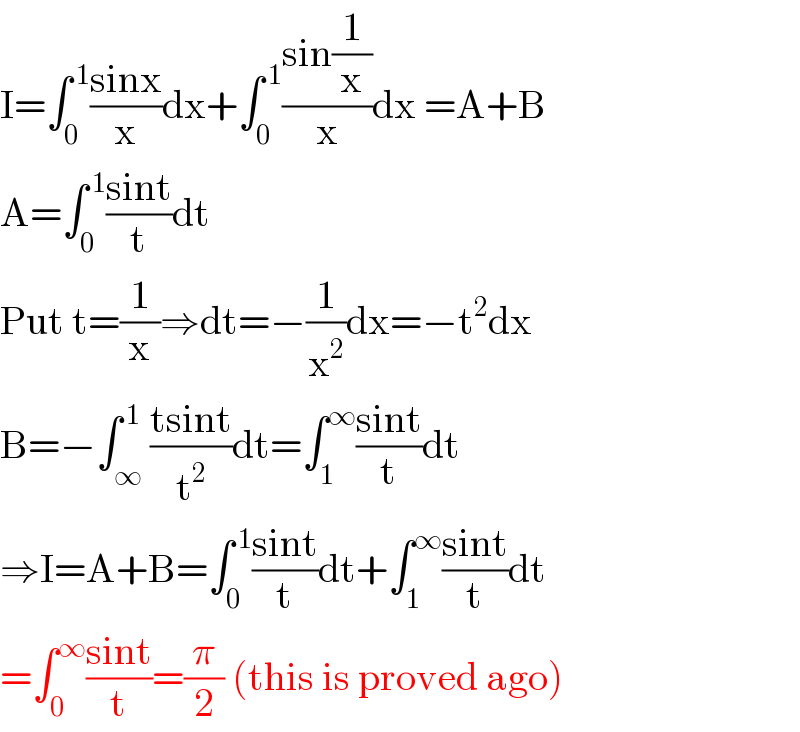
I=∫_0 ^( 1) ((sinx)/x)dx+∫_0 ^( 1) ((sin(1/x))/x)dx =A+B A=∫_0 ^( 1) ((sint)/t)dt Put t=(1/x)⇒dt=−(1/x^2 )dx=−t^2 dx B=−∫_∞ ^( 1) ((tsint)/t^2 )dt=∫_1 ^∞ ((sint)/t)dt ⇒I=A+B=∫_0 ^( 1) ((sint)/t)dt+∫_1 ^∞ ((sint)/t)dt =∫_0 ^∞ ((sint)/t)=(π/2) (this is proved ago)

$$\mathrm{I}=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{sinx}}{\mathrm{x}}\mathrm{dx}+\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{sin}\frac{\mathrm{1}}{\mathrm{x}}}{\mathrm{x}}\mathrm{dx}\:=\mathrm{A}+\mathrm{B} \\ $$$$\mathrm{A}=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{sint}}{\mathrm{t}}\mathrm{dt} \\ $$$$\mathrm{Put}\:\mathrm{t}=\frac{\mathrm{1}}{\mathrm{x}}\Rightarrow\mathrm{dt}=−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{dx}=−\mathrm{t}^{\mathrm{2}} \mathrm{dx} \\ $$$$\mathrm{B}=−\int_{\infty} ^{\:\mathrm{1}} \frac{\mathrm{tsint}}{\mathrm{t}^{\mathrm{2}} }\mathrm{dt}=\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{sint}}{\mathrm{t}}\mathrm{dt} \\ $$$$\Rightarrow\mathrm{I}=\mathrm{A}+\mathrm{B}=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{sint}}{\mathrm{t}}\mathrm{dt}+\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{sint}}{\mathrm{t}}\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sint}}{\mathrm{t}}=\frac{\pi}{\mathrm{2}}\:\left(\mathrm{this}\:\mathrm{is}\:\mathrm{proved}\:\mathrm{ago}\right) \\ $$

Commented by mnjuly1970 last updated on 14/Oct/20

$${mercey}.. \\ $$

Answered by mindispower last updated on 14/Oct/20

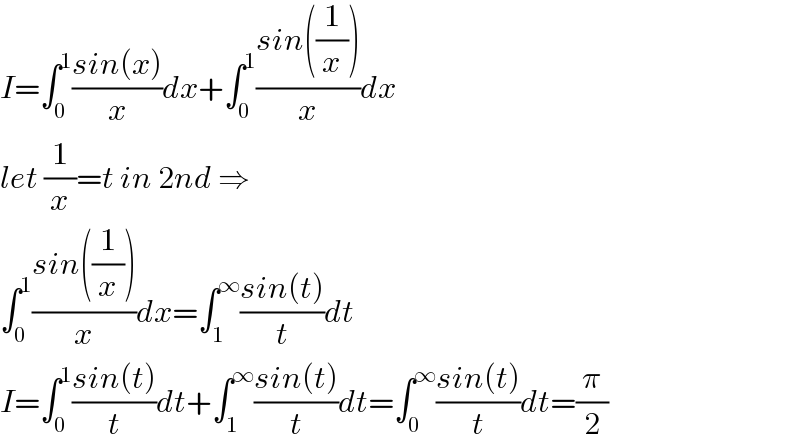
I=∫_0 ^1 ((sin(x))/x)dx+∫_0 ^1 ((sin((1/x)))/x)dx let (1/x)=t in 2nd ⇒ ∫_0 ^1 ((sin((1/x)))/x)dx=∫_1 ^∞ ((sin(t))/t)dt I=∫_0 ^1 ((sin(t))/t)dt+∫_1 ^∞ ((sin(t))/t)dt=∫_0 ^∞ ((sin(t))/t)dt=(π/2)

$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{sin}\left({x}\right)}{{x}}{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{sin}\left(\frac{\mathrm{1}}{{x}}\right)}{{x}}{dx} \\ $$$${let}\:\frac{\mathrm{1}}{{x}}={t}\:{in}\:\mathrm{2}{nd}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{sin}\left(\frac{\mathrm{1}}{{x}}\right)}{{x}}{dx}=\int_{\mathrm{1}} ^{\infty} \frac{{sin}\left({t}\right)}{{t}}{dt} \\ $$$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{sin}\left({t}\right)}{{t}}{dt}+\int_{\mathrm{1}} ^{\infty} \frac{{sin}\left({t}\right)}{{t}}{dt}=\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({t}\right)}{{t}}{dt}=\frac{\pi}{\mathrm{2}} \\ $$

Commented by mnjuly1970 last updated on 14/Oct/20

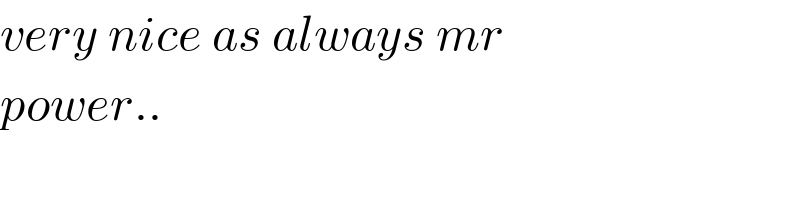
$${very}\:{nice}\:{as}\:{always}\:{mr} \\ $$$${power}.. \\ $$

Facebook Tweet Pin

nice-integral-please-evaluate-I-0-1-sin-x-sin-1-x-dx-x-m-n-1970-

Leave a Reply Cancel reply