Question Number 159474 by mnjuly1970 last updated on 17/Nov/21
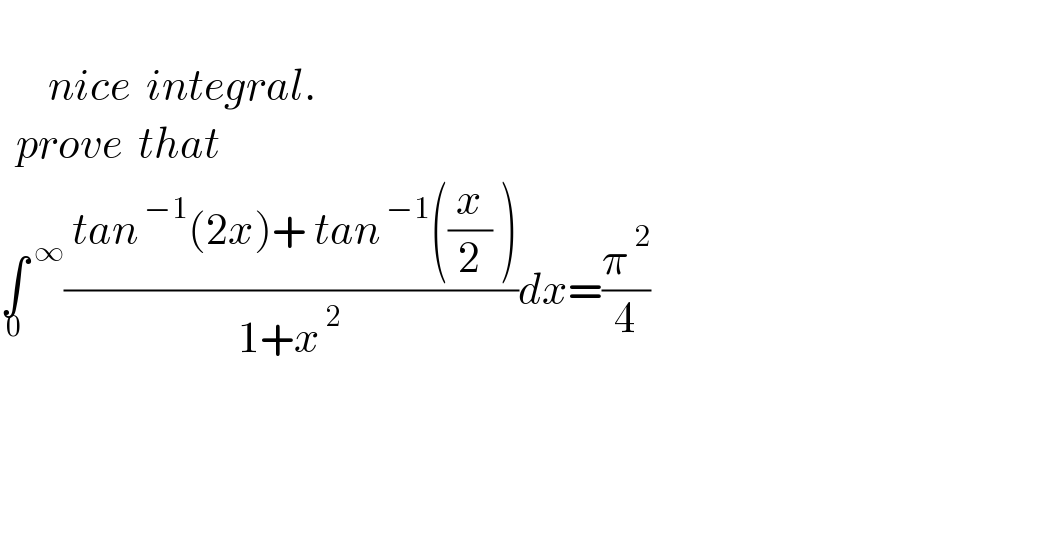
$$ \\ $$$$\:\:\:\:\:\:{nice}\:\:{integral}. \\ $$$$\:\:{prove}\:\:{that} \\ $$$$\underset{\mathrm{0}} {\int}^{\:\infty} \frac{\:{tan}^{\:−\mathrm{1}} \left(\mathrm{2}{x}\right)+\:{tan}^{\:−\mathrm{1}} \left(\frac{{x}}{\mathrm{2}}\:\right)}{\mathrm{1}+{x}^{\:\mathrm{2}} }{dx}=\frac{\pi^{\:\mathrm{2}} }{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\: \\ $$$$ \\ $$$$ \\ $$
Answered by qaz last updated on 18/Nov/21
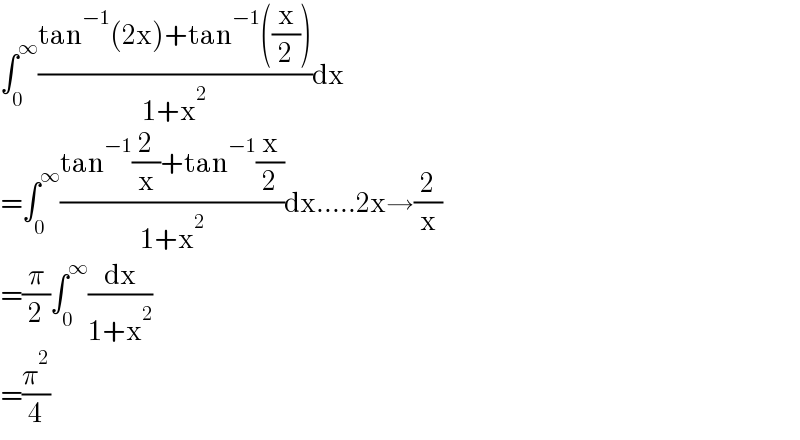
$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2x}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{x}}+\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{x}}{\mathrm{2}}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}…..\mathrm{2x}\rightarrow\frac{\mathrm{2}}{\mathrm{x}} \\ $$$$=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$
